 Hogyan lehet
ez, hiszen az eddigiek szerint mindaddig, amíg az erő
hat, növekednie kell a sebességnek?!
Miért nem haladhat bizonyos sebességnél
gyorsabban a vonat, akármennyire erőlködik is a mozdony?
Hogyan lehet
ez, hiszen az eddigiek szerint mindaddig, amíg az erő
hat, növekednie kell a sebességnek?!
Miért nem haladhat bizonyos sebességnél
gyorsabban a vonat, akármennyire erőlködik is a mozdony? A mozgás örök ellensége: a súrlódás
Mindennapi tapasztalatok - érdekes kérdések
Naponta találkozunk egyszerű kérdésekkel, amelyekre aligha tudunk megindokolt
feleletet adni. Íme néhány:
Egy korcsolyázó nekifut, azután szabadon siklik tovább. Mikor jut
messzebbre? Akkor, ha mindkét lábon állva mindkét korcsolyájának a talpa
súrlódik a jéghez,
vagy ha féllábon áll és csak az egyik korcsolyán csúszik tovább?
Legtöbben úgy gondolják, hogy messzebbre siklik akkor, ha féllábon áll, mert
akkor csak egy korcsolyatalpra hat a súrlódás
akadályozóereje, feltéve, hogy a jég olyan kemény, hogy a korcsolya nem vágódik
bele a jégbe.
A második kérdés hasonló: milyen szánkó csúszik könnyebben a havon, a széles
talpú vagy a keskeny talpú?
Érzés szerint az emberek többsége a széles talpú szánra szavaz. A szán és az
előbbi korcsolya esete ugyanaz, mégis korcsolya esetén a féllábú siklás, a kisebb
súrlódófelület látszik
előnyösebbnek, szán esetén pedig a szélesebb szántalp, a nagyobb súrlódófelület.
Majd kiderül, hol az igazság.
Az órákban leggyakrabban a billegőkerék
tengelye törik el azért, mert roppant vékony ez a tengely. Miért nem
készítik vastagabb tengellyel? Sejtjük, hogy azért, mert a vékony tengelyű
kerék könnyebben mozog.
De miért? Ezt aligha tudnánk megokolni. És ha állításunk Igaz, akkor az is előnyös,
hogy a kocsikerékbe minél vékonyabb tengelyt alkalmazzunk. Annál könnyebb húzni
a kocsit. Igaz ez is? És ha igaz, miért igaz?
A vonatot a mozdony húzza több ezer kilogrammsúly erővel.
Az állandó erő hatása
alatt a vonat sebessége
egyre növekedik. De egyszer csak már nem nő tovább a sebesség,
hanem a vonat ugyanakkora, változatlan sebességgel
halad tova, pedig az a több ezer kilogrammos húzóerő
akkor is hat.
 Hogyan lehet
ez, hiszen az eddigiek szerint mindaddig, amíg az erő
hat, növekednie kell a sebességnek?!
Miért nem haladhat bizonyos sebességnél
gyorsabban a vonat, akármennyire erőlködik is a mozdony?
Hogyan lehet
ez, hiszen az eddigiek szerint mindaddig, amíg az erő
hat, növekednie kell a sebességnek?!
Miért nem haladhat bizonyos sebességnél
gyorsabban a vonat, akármennyire erőlködik is a mozdony?
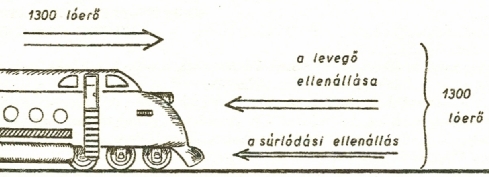
Meddig tud csak gyorsulni ez az 1300 lóerős mozdony? - Addig, amíg akkora végsebességet ér el, hogy az a munkavégzés, amit másodpercenként az akadályozóerők legyőzésére fordít, éppen 1300 lóerő lesz
Erre azonnal megfelelhetünk eddigi tudásunk alapján is. Ha nem lenne akadályozóerő
a vonat mozgásának útjában, akkor valóban tovább nőne a sebessége.
De ott van a súrlódás,
meg a levegő ellenállása. Mennél sebesebben halad a vonat, annál hosszabb
úton győzi le az akadályozó erőket
a mozdony, annál nagyobb munkát
végez másodpercenként. Végül egy bizonyos sebesség
elérésekor ez a munkavégzés
olyan nagy lesz, aminél nagyobbat a mozdony nem tud végezni. Ettől a pillanattól
kezdve a mozdony nem tudja tovább gyorsítani a vonatot, hiszen minden munkavégző
képességét a már elért sebességnél
felmerülő akadályozóerők
legyőzésére használja fel.
De azonnal felmerül a még érdekesebb kérdés:
Mekkora az a határsebesség,
amelynél sebesebben mér nem tudja mozgatni például az 500 lóerős
mozdony az 500 tonnás vonatot? Hogyan lehet ezt kiszámítani?
Annak számára, aki szeret kerékpározni, sokkal érdekesebb lesz, ha az előző
kérdést a kerékpárra alkalmazzuk. Tudjuk, hogy az erős testi munkás napi 8 órai
munkaidőben átlagosan 6 méterkilogrammsúly munkát
tud végezni másodpercenként. Ha a kerékpáros akkora munkát
végez kerékpár hajtása közben, mint az erős testi munkás, mekkora sebességgel
haladhat a jó úton? Mekkora utat tehet meg 8 órás munkaidőben?
A feltett kérdések a korcsolyázótól kezdve a vékony óratengelyen keresztül az
erős testi munkát végző kerékpáros sebességéig
- mind szorosan összefüggenek egymással. Ha könyvünknek ezt a fejezetét átolvassuk,
világosan látunk ezekben a kérdésekben.
Mit tanulunk szekrénytolás közben?
Ha nehéz, fából készült szekrényt sima fapadlón odább akarunk tolni, nehezen megy. Jól neki kell feküdni. Ennek oka az, hogy amikor fából készült tárgyat fából készült alapzaton akarunk továbbcsúsztatni, kb. akkora erőt kell kifejtenünk, mint az illető tárgy súlyának a 40%-a. Ha tehát az a szekrény 100 kilogramm súlyú, akkor 40 kilogrammsúly tolóerő szükséges a továbbcsúsztatásához.

A szekrény eltolásához ugyanakkora erőt kell kifejtenünk, akár a kisebb felületű oldalán fekszik, akár a nagyobb felületűn
Jegyezzük meg, hogy ha fa fán csúszik egyenletesen, akkor a súrlódásból
származó, a mozgást akadályozó erő,
röviden a súrlódás
40%.
A szekrényt lábain állva szokás odábbcsúsztatni. Könnyebben tudnánk-e a szekrényt
odábbesúsztatni, ha nem a kis felületű lábakon állana, hanem egyik oldallapjára
vagy a hátsó nagy lapjára fektetnénk a szekrényt?
Erre úgy adhatunk egészen bizonyos feleletet, ha kísérletet végeznénk. Egy rugós
erőmérővel megmérnénk azt az erőt,
ami szükséges a szekrény egyenletes, lassú továbbmozgatásához akkor, ha a kisebbik
oldalán, és akkor is, amikor a nagyobbik oldalán fekszik.
Azt látnánk, hogy az erőmérő mindegyik esetben ugyanakkora erőt
mutatna.
Meglepő és nagyon fontos törvényt találtunk:
a súrlódás nagysága nem függ attól, hogy a két test (példánkban a szekrény és a padló) mekkora felületen súrlódik egymáshoz.
A korcsolya és a szán súrlódása
Ha ezt tudjuk, akkor meg tudunk felelni a korcsolyázó és a szán problémájára.
Egészen mindegy, hogy az a lendületet vett korcsolyázó fél lábon vagy két lábon
siklik-e tovább. Mindkét esetben egyenlő messzire jut el. Ugyanis a mozgását
akadályozó erő mindkét
esetben ugyanakkora, függetlenül attól, hogy egy vagy két korcsolyatalp súrlódik-e
a jéghez.
Az is mindegy, hogy széles vagy keskeny a szán talpa, mindkét esetben ugyanakkora
a mozgást akadályozó súrlódás
a szán talpa és a hó között, ugyanakkora erő
kell a szán egyenletes mozgatásához.
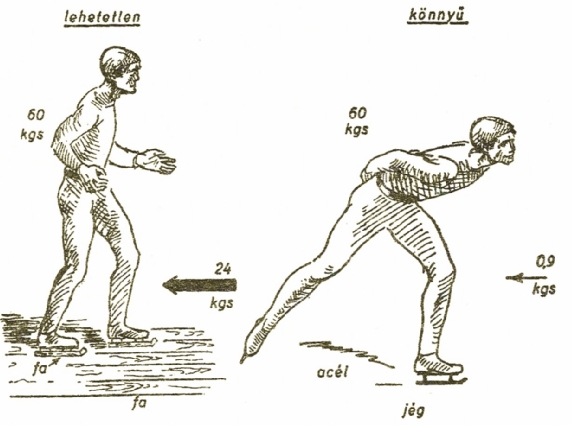
Ha fakorcsolyával fapadlón akarna korcsolyázni a 60 kg súlyú korcsolyázó, akkor 24 kgs mozgatóerőt kellene kifejtenie a súrlódás legyőzésére. Jégen acélkorcsolyával még 1 kgs erő se kell
Térjünk vissza a korcsolyához. Tudnánk-e fából készült korcsolyával simára
gyalult fapadlón siklani? Nem sikerülne, mert ha a korcsolyázó 60 kg súlyú
lenne, ennek 40%-át, azaz 24 kgsúlynyi erőt
kellene kifejteni a súrlódás
legyőzésére (ábra).
De ha az acélkorcsolya
jéggel érintkezik, az acél
és a jég között a súrlódás
a csúszó test súlyának csak 1,5%-a. Ezért a 100 kg súlyú embert is igen könnyen
el lehet tolni a jégen, ha korcsolyán áll, mert a 100 kgsúlynak csak 1,5%-a,
tehát 1,5 kg erő szükséges.
Ezért haladhatunk olyan sebesen korcsolyázás közben, pedig kis erőt
fejtünk ki.
Mekkora sebességgel tud haladni a korcsolyázó?
Most pedig nagyon érdekes és tanulságos feladat következik. A korcsolyázó kevesebb
erőkifejtéssel gyorsabban halad, mint a gyalogos. Ugyanezt tapasztaljuk kerékpározás
közben is.
Mekkora munkát végzünk
korcsolyázás, kerékpározás közben? Melyik a kevesebb munkát
kívánó közlekedési módszer? Teljes erőkifejtéssel
korcsolyázva vagy kerékpározva haladunk sebesebben? Mekkora ez a sebesség?
Számításunk újra könnyű lesz. Egyszerűség kedvéért mozgás közben csak a súrlódást
vesszük tekintetbe.
A korcsolyázó. - Tegyük fel, hegy kényelmesen halad, csak akkora sebességgel,
mint a siető gyalogos, aki óránként körülbelül 7 kilométert, másodpercenként
2 méter utat tesz meg vízszintes úton. - Mekkora munkát végez, ha súlya 60 kilogramm?
Tudjuk, hogy miközben az acél a jéghez súrlódik, a mozgást a súrlódás akkora
erővel akadályozza, mint amekkora a test súlyának 1,5%-a.
60 kgsúlynak 1,5%-a = 0,9 kgs kb. 1 kilogrammsúly.
Ezért annak a korcsolyázónak korcsolyázás közben a súrlódás 1 kgsúlynyi akadályozóerejét
kell legyőznie, mégpedig másodpercenként 2 méter úton,
1 kgsúly . 2 méter = 2 méterkilogrammsúly.
Az erős testi munkás napi 8 órán keresztül 6 méterkilogrammsúly munkát
tud végezni másodpercenként. Az óránként 7 km sebességgel
haladó korcsolyázó háromszor kevesebb munkát
végez.
Ha tehát a korcsolyázó olyan munkateljesítményt
akar kifejteni korcsolyázás közben, mint az erős testi munkás, vagyis 2 méterkilogrammsúly
helyett 6 méterkilogrammsúlyt, akkor másodpercenként nem 2, hanem 6 méter úton
győzi le a súrlódás
1 kilogrammnyi akadályozóerejét. Egy óra alatt háromszor több utat tesz meg,
mint előbb, 7 km . 3 = 21 kilométert.
Az erős testi munkás teljesítményével dolgozó korcsolyázó óránként 21 km utat
tesz meg, feltéve, hogy csak a súrlódás
hat mint akadályozóerő.
(Ha a levegő ellenállását is tekintetbe vennénk, akkor nagyobb lenne az akadályozóerő,
kisebb a sebesség.)
A példa nyomán teljesen világos, hogy miért nem fokozódhat egyszer csak tovább
a korcsolyázó sebessége,
bár teljes erőkifejtéssel
dolgozik. Ugyanis mozgás közben le kell győznie a súrlódás
akadályozóerejét - eközben munkát
végez. Az egy másodperc alatt végzett munkát
könnyen kiszámíthatjuk, ha tudjuk, hogy másodpercenként hány méter utat tesz
meg és mekkora erőt győz
le. A kettő szorzata adja a szükséges teljesítményt. A sebesség
csak addig növekedhetik, míg végül az így számított teljesítmény eléri a mozgáshoz
rendelkezésünkre álló teljesítményt. Ezután már nem növekedhet tovább a sebesség,
hiszen a mozgás közben végzett munka
teljesen felemészti a rendelkezésre álló munkavégző
képességet.
Lemaradna-e a kerékpáros a korcsolyázó mögött?
Most már magunk is könnyen meg tudnánk felelni a kerékpárosra vonatkozó hasonló
kérdésre: milyen sebesen halad az a kerékpáros, aki úgy dolgozik, mint az erős
testi munkás?
Tudnunk kell, hogy mekkora a súrlódás
kerékpározáskor. Sima betonúton 3%.
Korcsolyázáskor 1,5% a súrlódás,
kerékpározáskor 3%, vagyis kétszer több. Ezért a kerékpárost még kitűnő úton
is kétszer nagyobb súrlódás
akadályozza mozgásában, mint a korcsolyázót. Mivel az ellenállás, a legyőzendő
erő kétszer nagyobb,
azért ugyanannyi idő alatt kétszer kisebb utat tesz meg a kerékpáros, mint a
korcsolyázó, ha másodpercenként 6 méterkilogrammsúly munkát
végez. Tehát óránként nem 21 kilométert, hanem ennek csak a felét, mintegy 10
kilométert tesz meg. (Ezt az eredményt véglegesnek fogadhatjuk el, mert ilyen
aránylag kis sebesség
esetén a levegő ellenállása nem lényeges.)
Aki már kerékpározott egész napon át, az saját tapasztalata alapján is megerősítheti
eredményünket: ha valaki szélcsendes
időben, kitűnő, vízszintes betonúton napi 8 óra alatt 8 .
10 = 80 km utat tesz meg kerékpáron, akkor egy erős testi munkás napi munkáját
végzi el.
Nem is olyan kis munka
a kerékpározás, főleg ha valaki naponta néhány órát kénytelen kerékpározni.
Ma már a sűrű autóbuszjáratok ettől is megkímélik a vidéki dolgozókat.
Példáink bizonyítják, milyen fontos az, hogy mozgások esetén csökkentsük a kikerülhetetlen súrlódást. Mivel mindenki nagyon jól tudja, azért csak megemlítjük, hogy a csúszósúrlódást kenőszerek (pl. olaj) alkalmazásával csökkenteni lehet, de a legjobb eljárás az, ha a csúszósúrlódást gördülősúrlódássá alakítjuk át, pl. a nehéz tárgy alá tett hengerek alkalmazásával Ilyenkor 50-ed, 100-ad résznyi erő is elegendő a mozgatáshoz.
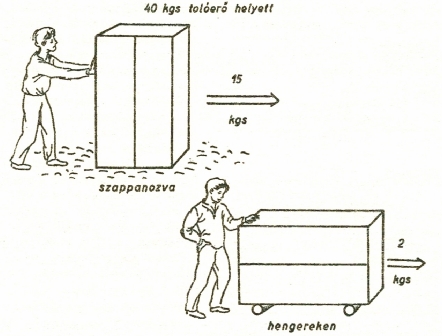
A súrlódás nagyságát csökkenthetjük alkalmas kenőszerrel.
Legcélszerűbb gördülősúrlódássá változtatni a csúszósúrlódást
Hány százaléka a test súlyának a súrlódási erő?
|
Szárazon
|
Kenőszerrel
|
Vízzel nedvesítve
|
|
| Vas vason csúszik |
10
|
1
|
-
|
| Fém fán csúszik |
50-60
|
20
|
25
|
| Fa fán csúszik |
50-20
|
20
|
25
|
| Bőrszíj öntöttvason |
50
|
18
|
38
|
| Vas jégen csúszik |
-
|
-
|
1,5
|
| Lefékezett gépkocsi kövezeten |
50
|
-
|
20
|
| Lefékezett gépkocsi aszfalton |
30
|
-
|
15
|
Ha a nehéz tárgyat az alája tett hengereken gördítjük, valóban elkerüljük a
csúszó ellenállást, De kiküszöböljük-e akkor is a csúszó ellenállást, ha kereket
alkalmazunk?
Nem! A kerék egészen más, mint a nehéz tárgy alá tett henger. A kerékben
megmarad a csúszósúrlódás,
hiszen a kerék tengelye és a kerék agya között csúszósúrlódás
van. Igaz, hogy kenéssel csökkenthetjük a súrlódást,
de végeredményben a kerék nem küszöböli ki a csúszósúrlódást.
Akkor miért tartozik a kerék a legnagyobb találmányok közé? Mi a kerék
működésének a lényege? Erről valóban csak kevés embernek van fogalma. A következő
egyszerű példán könnyen megértjük.
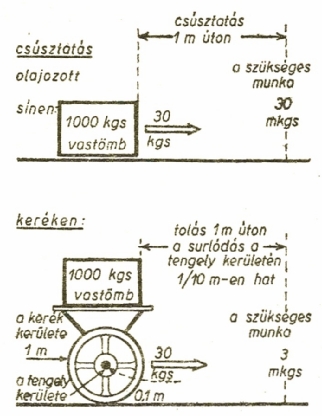 1000 kg
súlyú vastömböt kell odábbcsúsztatnunk jól megolajozott vassíneken. Ilyenkor
a súrlódás 3%. Ezért
az 1000 kg-os vastömb csúsztatásához 30 kgsúly erő
szükséges. Ha 1 méternyi úton át csúsztatjuk, a végzett munka
30 kgsúly .1 m = 30 méterkilogrammsúly.
1000 kg
súlyú vastömböt kell odábbcsúsztatnunk jól megolajozott vassíneken. Ilyenkor
a súrlódás 3%. Ezért
az 1000 kg-os vastömb csúsztatásához 30 kgsúly erő
szükséges. Ha 1 méternyi úton át csúsztatjuk, a végzett munka
30 kgsúly .1 m = 30 méterkilogrammsúly.
Tegyünk kereket a vastömb alá. A kerék acéltengelye olajozott acél csapágyon
nyugszik. Mekkora súrlódást kell most legyőzni a tengely kerületén?
A kerék előnye: a vékony tengely kis kerületén kell legyőzni a súrlódást a kerék egy fordulata alatt
Mivel megint acél csúszik olajozott acélon, azért a súrlódás változatlanul
marad 3%.
Tegyük fel, hogy a kerék kerülete 1 méter, a kerék tengelyének kerülete pedig
tizedrésze a kerék kerületének. Mekkora munkát kell most végezni, mialatt 1
méterrel odábbmozdítjuk a vastömböt?
Ezalatt a kerék egyet fordul, közben a tengely kerületén kell legyőzni a súrlódást.
De a tengely kerülete tizedrésze a kerék kerületének, 0,1 méter. Ezért a tengely
kerületén végzett súrlódási munka tizedrésze az előbb számított 30 méterkilogrammsúlynyi
munkának, és ezalatt a vastömb megint 1 méterrel jutott tovább.
Gondoljuk át a két eredményt:
30 méterkilogrammsúly a végzett munka, ha sínen csúsztatjuk
a vastömböt.
3 méterkilogrammsúly a végzett munka, vagyis tízszer kevesebb, ha olyan kereket
alkalmazunk, amelyben a tengely kerülete tízszer kisebb, mint a kerék kerülete.
De a keréknek még vékonyabb tengelyt is készíthetünk. Legyen a tengely vastagsága
századrésze a kerék átmérőjének. Akkor az előbbi 30 kgs súrlódási ellenállást
100-szor rövidebb úton kell legyőzni, mint kerék nélkül csúsztatással, a végzett
munka 100-szor kisebb lesz. A vastömb mozgatása 100-szor kisebb erőt kíván,
ha ilyen kereket alkalmazunk.
Ez valóban meglepő. - És mi történik, ha egy kocsi tengelyére kétszer, háromszor
nagyobb kerületű (átmérőjű) kereket szerelünk, mint előbb volt rajta?
Akkor a kocsit kétszer, háromszor kisebb erővel,
kétszer, háromszor kevesebb munkavégzéssel
lehet mozgatni. Ezért húzza a ló könnyebben a nagyobb kerekű kocsit. Ezért
igyekeznek az órában is a kerekeket olyan vékony tengellyel ellátni, amilyennel
csak lehetséges. Annál kevesebb munkát
kíván a kerék forgatása.
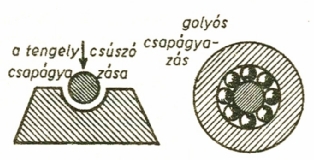 De még a
forgó tengelynek a csapágyon való súrlódását is kiküszöböli a golyóscsapágy.
Ha a tengelyt golyóscsapágyba helyezzük, nem csúszik, hanem gördül az acélgolyókon.
De még a
forgó tengelynek a csapágyon való súrlódását is kiküszöböli a golyóscsapágy.
Ha a tengelyt golyóscsapágyba helyezzük, nem csúszik, hanem gördül az acélgolyókon.
Ha golyóscsapágyat alkalmazunk, a súrlódás 50-szer is kisebb lehet, mint az a súrlódás, amely a közönséges csúszócsapágyban fellép
Mennyivel jobb a golyóscsapágy, mint a közönséges csúszócsapágy? Ha golyóscsapágyat
alkalmazunk, akkor a súrlódás
50-szer is kisebb lehet!
A "csoda" egyetlen összehasonlításban nyilvánvaló lesz. Ha egy tíz
tonnás (10 000 kg) acéltömböt
sínekre helyeznénk és lassan csúsztatnánk, közben a súrlódás
10%-os ellenállását kellene legyőzni, tehát 1000 kgsúly erőt
kellene kifejteni.
A tíz tonnás vasúti kocsi kerekeken és sínen mozoghat. A vagon tolásához
csak akkora erőt kellene
kifejteni, mint a vagon súlyának 0,2%-a, tehát 20 kgsúly erőt.
Ha kereket alkalmazunk, akkor ugyanakkora erővel
50-szer több anyagmennyiséget tudunk egyenletesen továbbmozgatni a sínen, mint
kerék nélkül.
A következő táblázatból megtudhatjuk, hogy közismert járműveinket mekkora erővel lehet egyenletesen, lassan mozgatni vízszintes pályán.
A gördülsúrlódás
(A kerekes járművek mozgatásához szükséges erő súlyuk százalékában)
| Vasalt kerék földúton halad |
20
|
| Vasalt kerék betonúton halad |
1
|
| Vasalt kerék jó földúton halad |
5
|
| Légtömlős kerék betonúton halad |
3
|
| Légtömlős kerék földúton halad |
4,5
|
|
Villamoskocsi |
0,6
|
| Vasút |
0,2
|
| Gépkocsi kövezeten |
4
|
| Gépkocsi aszfalton |
3,5
|
| Gépkocsi betonon |
3
|
Példa. Már bizonyára láttuk, hogy a gépkocsivezető a leállított kocsit kissé
odábbtolja. Jól neki kell feküdnie. Valóban nagy erőt
kíván a kocsi továbbtolása? Számítsuk ki .
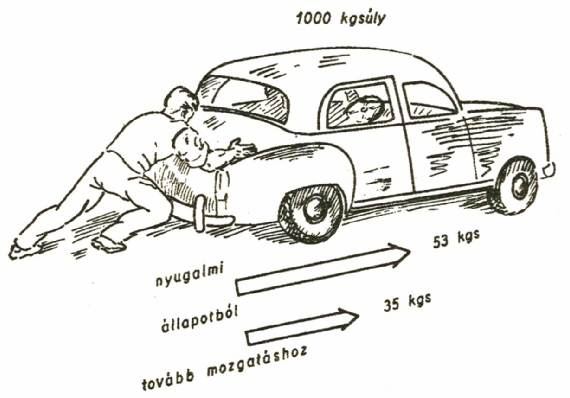 A nyugalomban
levő kocsi megmozdítása (a nyugalmi súrlódás legyőzése) nagyobb erőt
kíván, mint a kocsi lassú tolása
A nyugalomban
levő kocsi megmozdítása (a nyugalmi súrlódás legyőzése) nagyobb erőt
kíván, mint a kocsi lassú tolása
Egy kisautó súlya 1000 kg. Továbbtolása aszfalton 3,5% erőt kíván. 1000 kilogrammsúly 3,5%-a 35 kgsúly. Tehát a kocsi egyenletes lassú mozgatásához 35 kgsúly erő szükséges. De tapasztalatból tudjuk, hogy mielőtt a test csúszni vagy gördülni kezd, még nagyobb erőt kell kifejteni ahhoz, hogy nyugalmi állapotból mozgásba jöjjön A "nyugalmi" súrlódás általában 50%-kal nagyobb mint a mozgás közben tapasztalt súrlódás. Tehát a gépkocsi tolására az első pillanatban 35 kgs + 17,5 kgs 52,5 kgs-nyi, vagyis félmázsányi nyomóerőt kell kifejteni. Tapasztalatunk igazolja a számítás eredményét.