 Amekkora erővel
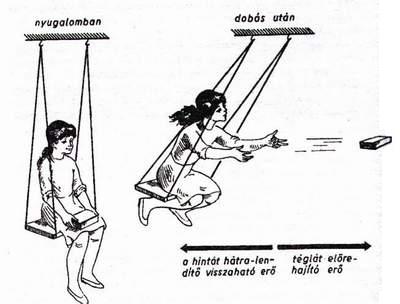
a hintán ülő előre dobja a téglát, ugynakkora erő löki a hintát ellenkező irányba.
Amekkora erővel
a hintán ülő előre dobja a téglát, ugynakkora erő löki a hintát ellenkező irányba.Mi hajtja a rakétát? - Miért rúg a puska?
A hatás - ellenhatás törvénye
Ma a rakéták általános érdeklődést keltenek. Könyvünk első részében már annak kiszámítását is megtanultuk, hogy például mekkora erőnek kell hatnia, hogy az 1000 kg tömegű rakétának 10 másodperc alatt 1 kilométer másodpercenkénti végsebességet adjon. Csak arról nem volt még szó, miként állítjuk elő azt az erőt, ami majd hajtja a rakétát. Erről lesz szó most. Könnyen érthető és nagyon hasznos lesz minden, mert világosabban látunk majd sok mindent, amit a rakétáról hallunk.
 Amekkora erővel
a hintán ülő előre dobja a téglát, ugynakkora erő löki a hintát ellenkező irányba.
Amekkora erővel
a hintán ülő előre dobja a téglát, ugynakkora erő löki a hintát ellenkező irányba.
Kezdjük el néhány közismert tapasztalattal. Ha a csónakból partra ugrunk, a
csónakot ellenkező irányú lökés éri, ellökődik a parttól. Ha a mozdulatlan hintán
ülünk és előre hajítunk egy téglát (a fenti ábra szerint), magunk is ellökődünk
az ellenkező irányba. Ha a fegyvert elsütjük, a lőporgázok nyomóereje előre
mozgatja a lövedéket, de ugyanakkor hátrafelé mozgatja a fegyvert, rúgást érzünk.
A forgó pázsitpermetező vízszintesen álló csövének oldalán nyílások vannak.
A nyíláson át oldalt kiszökell a víz
a cső pedig ellenkező irányú forgásba jön. A kilövellő víz ellenhatása hozza
forgásba.
Mennyiben jelentenek az előbb említett példák valami újat ahhoz képest, amit
eddíg is tudtunk az erőről?
Eddig is tudtuk azt, hogy erőről csak akkor beszélhetünk, ha két test van jelen.
Az erő ennek a két testnek (pl. a hintán ülő embernek és az elhajított téglának)
egymásra hatása. De eddig azt hihettük, hogy lehetséges az, hogy csak
az egyik test hasson a másikra (pl. csak az ember löki a téglát).
A felsorolt mindennapi példák azt bizonyítják, hogy ez lehetetlen. Lehetetlen
az, hogy csak az egyik test hasson a másikra. Lehetetlenség egyetlen erő elképzelése.
Az erők mindíg párosával lépnek fel a természetben !
Lehetetlen az, hogy csak a hintán ülő ember lökje előre a követ, a kő
is löki visszafelé az embert.
A hatóerővel szemben mindíg fellép az ellenkező irányú visszahatóerő (a reakcióerő).
Mekkora a visszaható erő nagysága
Igen hatásos és egyszerű kísérletekkel be lehet bizonyítani, hogy a visszaható
erő pontosan ugyanakkora, mint a hatóerő.
Egy érdekes példa: van olyan ágyú, amely 100 kg súlyú lövedéket 1,5 km-es másodpercenkénti
sebességgel lő ki. Miközben a lövedék az ágyúcsőben mozog, a lőporgázok 600.000
kgsúly erővel mozgatják. De ugyanekkor a lőporgázok az ágyúcsövet ugyancsak
600.000 kgsúly erővel nyomják hátrafelé. Gondoskodni kell arról, hogy a cső
állványa ezt kibírja, különben a visszaható erő a csövet letépi az állványról.
Tapasztalatainkat így foglalhatjuk törvénybe:
Ez a hatás-ellenhatás törvénye. Ezt a törvényt Newton fogalmazta meg 1687-ben, és az erőtan harmadik alptörvényének nevezzük.
Egy fogas kérdés, a ló és a kocsi
Az eddigi példák érthetőek voltak, a törvény is az. De mondok egy esetet, ki
tudja megmagyarázni?
A ló húzza a kocsit - A hatás-ellenhatás törvénye szerint a kocsi ugyanakkora erővel húzza visszafelé a lovat. Tehát a kocsiból és a lóból álló testre semmiféle erő nem hat. A kocsinak és a lónak nem lenne szabad elmozdulnia. Miért mozog mégis a kocsi?
 Miért
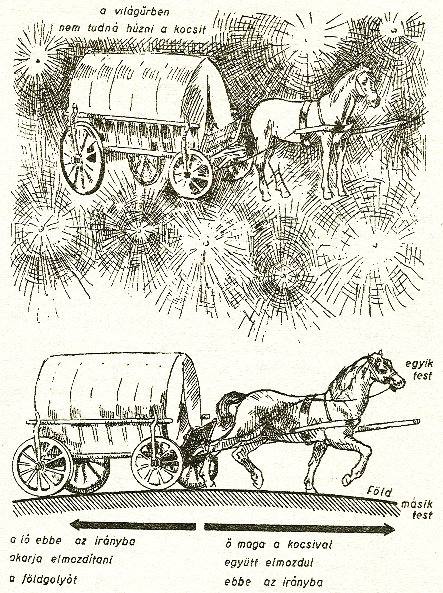
mozdul el a kocsi, ha húzza a ló? - A kocsi a lóval együtt elmozdul az egyik
irányba, a Föld pedig az ellenkező irányba
Miért
mozdul el a kocsi, ha húzza a ló? - A kocsi a lóval együtt elmozdul az egyik
irányba, a Föld pedig az ellenkező irányba
A ló patáival tulajdonképpen a Földgolyóra gyakorol erőt, el akarja mozdítani
a másik irányba. A Föld el is mozdul, a ló pedig a vele összekötött kocsival
elindul a másik irányba.
Hasonló a helyzet akkor is, ha követ hajítunk felfelé, például 50 méter
másodpercenkénti sebességgel. Ilyenkor a Föld is elmozdul a az ellenkező irányba,
de óriási tömege miatt sokkal kisebb sebességgel. Amikor pedig a kő Föld és
a kő vonzása miatt visszafelé esik, akkor nem csak a kő mozog a Föld felé,
hanem a Föld is a kő felé, végre találkoznak.
Természetesen ezekben az esetekben a Föld mozgásának sebessége roppant kicsiny.
Hogyan lehet kiszámítani a visszaható erő által okozott végsebességet?
Nagyon egyszerűen. Két péda alapján világosan megértjük, és fejben is szép
számításokat tudunk elvégezni.
A hintán ülő ember és az eldobott tégla. - Tegyük fel, hogy egy 60 kg
súlyú ember ül a hintán. Ültében 6 kg-os téglát dob előre. Mekkora sebességgel
lendül hátrafelé a hintán?
Az ember testének tömege (60 kg) tízszer akkora, mint a tégla tömege (6 kg).
Ezért az ember tízszer kisebb sebességgel lendül hátrafelé, mint amekkora sebességgel
előre löki a téglát.
Tegyük fel, hogy a téglát 10 méter másodpercenkénti
sebességgel hajította
előre. Akkor az ember sebessége
tízszer kisebb, azaz 1 méter másodpercenkénti
végsebességgel lendül
hátrafelé a dobás visszaható erejénél fogva.
Alkalmazzuk az előbbi egyszerű számítást egy lőfegyverre. Egy pillanat alatt ki lehet számítani, hogy mekkora sebességgel mozdul el hátrafelé a fegyver, és ebből azonnal tudjuk, hogy mennyire rúg (ábra).
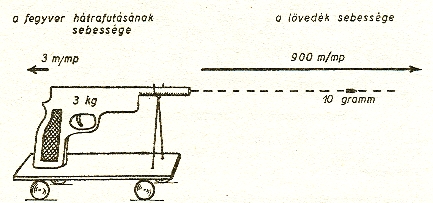 A lőporgáz
nyomóereje előre löki a lövedéket, de ugyanakkor hátralöki a fegyvert. A fegyver
sebessége 1 lövedék kilövése után
A lőporgáz
nyomóereje előre löki a lövedéket, de ugyanakkor hátralöki a fegyvert. A fegyver
sebessége 1 lövedék kilövése után
Legyen a fegyver súlya 3000 gramm (3kg), a lövedék súlya pedig 10 gramm. A
fegyver súlya a lövedék súlyánál 300-szor több. Ebből következik, hogy a fegyver
300-szor kisebb sebességgel mozogna hátrafelé (ha szabadon mozoghatna), mint
amekkora sebességgel kilövi a lövedéket.
Tegyük fel, hogy ez a lövedék 900 méter másodpercenkénti
sebességgel hagyja
el a fegyver csövét. Akkor a fegyver 300-szor kisebb sebességgel
fut hátrafelé. A 900-ban a 300 megvan 3-szor.
A fegyver 3 méter méter másodpercenkénti sebességgel fut hátrafelé.
Most már könnyű elképzelni a fegyver rúgásának nagyságát. Gondoljuk azt,
hogy az a 3 kg súlyú fegyver egy súlytalan, súrlódás nélkül mozgó kis kocsira
van erősítve. Ha elsütjük, akkor lövés után a fegyver olyan sebesen halad hátrafelé,
hogy másodpercenként 3 méter (óránként 10,8 km) utat tesz meg. Tehát kétszer
olyan sebesen haladna, mint a siető ember. Tartsuk a fegyver elé vállunkat.
Amennyire megüti, annyira rúg a fegyver.
Ugye milyen egyszerű. A világon minden ilyen egyszerű, ha megértjük. A tudományban
nincs nehéz és könnyű, csak megértett és meg nem értett dolgok vannak.
De megoldásaink még szebb része csak ezután következik. Tudásunkat a rakétára
alkalmazzuk. Ez is ugyanilyen világos és egyszerű lesz.
Képzeljük, hogy a puska ott van a súlytalan, súrlódás
nélkül mozgó kis kocsin. (De elképzelhetjük azt is, hogy ott van valahol a világmindenség
olyan helyén, ahol semmi erő
sem hat rá, tehát lebeg az űrben.)
A fegyver leadja az első lövését és 3 méter másodpercenkénti sebességgel elindúl
a lövéssel ellenkező irányban, ahogyan az ábrán látható.
Semmi akadálya sincs annak, hogy abból a fegyverből egymás után sok lövést adjunk
le. Képzeljük el, hogy a fegyver önműködő és akkor igazán kilőheti egymásután
a tölténytárban lévő összes töltényt.
De ennek érdekes következménye lesz. A fegyver egyre nagyobb sebességgel
fut az ellenkező irányba. Ugyanis minden lövés másodpercenkénti
3 méterrel növeli a fegyvernek már meglévő sebességét.
Mekkora lesz tehát a sebessége 10, 20, .... 100 lövés után?
Fejben, minden megerőltetés nélkül kiszámíthatjuk. Ha az első lövés után 3 m/mp
a sebessége, akkor
a második után 6 m/mp, a harmadik után 9 m/mp, tíz lövés után pedig 10
. 3 azaz 30 m/mp.
A tizedik lövés után a fegyver 108 km/óra sebességgel halad (mert egy óra =
3600 másodperc, 1 óra alatt tehát 3600 . 30 méter = 108.000 méter = 108 kilométer
utat tesz meg). A fegyver olyan sebességgel halad, ami megközelíti az autópályán
megengedett sebességet.
És mindez csak 10 lövés után!
Mekkora lesz a fegyver sebessége 100 lövés után?
Ha 10 tíz lövés után 108 km/óra, akkor 10-szer több, azaz 100 lövés után
10 . 108 km, tehát 1080 km óránként!
Aligha gondoltuk volna, hiszen ez már magasabb az utasszállító repülőgépek átlagsebességénél,
a hangsebesség közelében tartunk!
Igaz ez a könnyen elképzelhető példa éppen a rakétamozgást teszi számítással
érthetővé.
De kilőhet-e ez a fegyver 10 golyót magából?
Egy lövedék súlya példánkban 10 gramm volt. 100 lövedék súlya 1000 gramm, 1
kilogramm. Fegyverünkről azt mondtuk, hogy súlya a lövöldözés kezdetén 3 kilogramm.
100 lövés után a súlya 1 kilogrammal csökken csak, tehát a 3 kg-os fegyver valóban
kilőhet magából 100 lövedéket, és akkor számításunk szerint 1080 km-es óránkénti
sebességet ér el.
Már ez is tekintélyes sebesség. De a valóságban még ennél is nagyobb lesz
a fegyver sebessége.
Ki tudná megmondani, hogy miért?
Előző példánkban feltételeztük, hogy az egymást követő lövések alatt a fegyver
tömege változatlanul 3 kg marad. De a valóságban ez nincsen így, mert miközben
egy-egy lövedék eltávozik, a fegyver súlya (tömege) minden lövéskor 10 grammal
csökken. A századik lövés után már 1 kilogramnyi kilőtt lövedék súlyával
lesz könnyebb a fegyver, tehát a századik lövéskor már csak 2 kg az a tömeg,
amelynek a sebességét a visszaható erőnek növelnie kell. A fegyver egyre
csökkenő tömegének az egymásra következő lövések mindíg valamivel nagyobb sebességet
adnak, mint az előző lövés.
Ezért 100 lövés utána a fegyver sebessége több lesz, mint 1080 km óránként.
Elérheti-e a fegyver a belőle kilőtt golyók sebességét?
A fegyverünkből kilőtt golyók sebessége 900 m volt másodpercenként, 3240 km
óránként. Száz golyó kilövése után pedig a fegyver 1080 km óránkénti sebességet
ért el, ha a 3 kg-os fegyver tömegét közben változatlannak tételeztük fel.
De most vegyük tekintetbe azt is, hogy a fegyver tömege a lövések közben egyre
csökken. Elképzelhető-e, hogy annyi golyót lövünk ki a fegyverből, hogy végűI
a fegyver a kilőtt golyók sebességéve, 3240 km óránkénti sebbességgel repül?
Ez nagyon érdekes kérdés. A rakétatechnika
alapvető kérdése. A rá adott feleletet érdemes nagyon jól megjegyezni mert valóban
értékes tudást ad. A felelet:
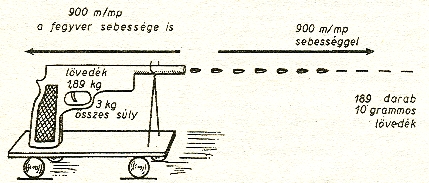 A fegyver
akkor éri el a belőle kilőtt lövedék sebességét,
ha eredeti súlyának, azaz a 3 kilogramnak 63 százalékát lövedékek alakjában
kilőnék belőle (ábra).
A fegyver
akkor éri el a belőle kilőtt lövedék sebességét,
ha eredeti súlyának, azaz a 3 kilogramnak 63 százalékát lövedékek alakjában
kilőnék belőle (ábra).
Mit jelent ez? A 3 kilogramm 63%-a 1890 gramm.
A 3 kgsúlyú fegyver tölténytárában tehát 1,89 kg (189 darab) tölténynek kellene
lennie. Magára a fegyver szerkezetére így rnidössze kb. 1,1 kg súly maradna.
189 lövés után az 1,1 kg súlyú üres fegyver 3240 km óránkénti (900 m másodpercenkénti)
sebességgel repülne
tova a lövedékkeI ellenkező irányba, a Iövedékek visszahatás következtében.
A rakéták belsejében könnyen égő anyagok vannak. Ezek égése közben a fejlődő
égésgázok részecskéi, mint parányi lövedékek, a rakéta nyílásán át nagy sebességgel
lövellnek ki és visszaható erejükkel egyre sebesebb mozgásba hozzák a rakétát.
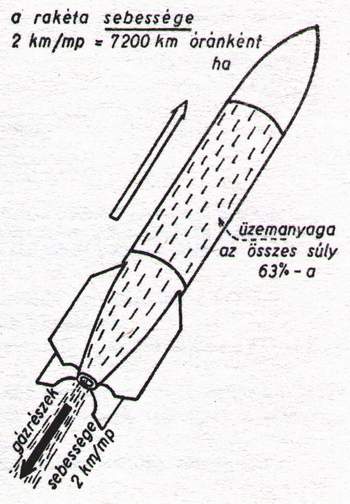
Alkalmazzuk előbbi egyszerű tételünket a rakétára.
Van egy 100 tonnás (100.000 kg súlyú) rakétánk. Azt akarjuk, hogy a rakéta akkora
sebességet érjen
el, mint amekkora sebességgel
az égésgázok távoznak belőle (ábra).
Egy 100.000 kg összsúlyú rakétának 63.000 kg üzemanyagot kell magával vinnie, ha azt akarjuk, hogy a rakéta akkora sebességgel haladjon, mint amekkora sebességgel az égési gázok kilövellnek belőle.
Mennyi tüzelőanyagot kell magával vinnie a rakétának?
A rakéta az egész tömegének a 63%-át a tüzelőanyagnak kell alkotnia.
Tegyük fel, hogy az égésgázok 2 km másodpercenkénti (7.200 km/órás) sebességgel
távoznak a rakétából.
Akkor a 63.000 kg üzemanyag elégetése után a visszamaradó 27.000 kg tömegű rakéta
óránként 7.200 km óránkénti sebességgel száguld, ha mozgását semmi sem akadályozza.
Ez az óránkénti 7.200 kilométeres sebesség, még mindíg csak negyedrésze a mesterséges
holdak kilövéséhez szükséges végsebességnek.