baricentrikus koordináta
(baricentrum)
Egy pont koordinátája olyan koordináta-rendszerben, amelynek kezdőpontja a
rendszer tömegközéppontjában (baricentrumában) van.
A baricentrikus koordináták használatával némely égi mechanikai összefüggés
egyszerűbben írható fel, mint más koordináta-rendszerben.
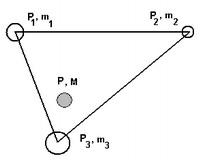Ha a síkban
a P1, P2, P3 pontok kifeszítik a síkot (nem
kollineárisak, nem esnek egy egyenesbe) és helyvektoruk v1, v2,
v3, akkor a sík bármely S pontjának s helyvektora előállítható ezek
súlyozott közepeként; azaz található hozzá olyan m1, m2,
m3 számhármas, amellyel a S pont s helyvektora:
| s = |
m1.v1 + m2.v2
+ m3.v3
|
= b1.v1 + b2.v2 + b3.v3; |
bi =
|
mi
|
|
----------------------------
|
-----------------------
|
|||
|
m1 + m2 + m3
|
m1 + m2 + m3
|
Az m1, m2, m3 számokat (illetve a b1, b2, b3 számokat) az S pont (-nak a P1, P2, P3 rendszerre vonatkozó) baricentrikus koordinátáinak nevezzük.
Szemléletesen: a Pi pontokba helyezett mi súlyok (tömegek) súlypontja (tömegközéppontja) S.
Ha mindhárom súly pozitív, a súlypont a háromszögön belül van; külső pontok
esetén vannak negatív súlyok is, és ha valamelyik súly 0, akkor a súlypont a
háromszögnek a megfelelő ponttal szemközti oldalán van.