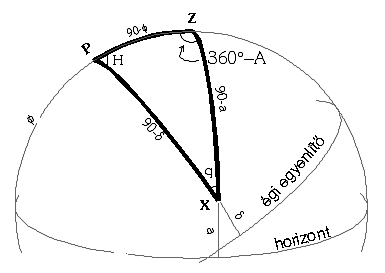
 A világpólus
(P), a zenit (Z) és valamely csillag (X) által meghatározott égi gömbháromszög.
A világpólus
(P), a zenit (Z) és valamely csillag (X) által meghatározott égi gömbháromszög.csillagászati gömbháromszög
 A világpólus
(P), a zenit (Z) és valamely csillag (X) által meghatározott égi gömbháromszög.
A világpólus
(P), a zenit (Z) és valamely csillag (X) által meghatározott égi gömbháromszög.
A háromszög oldalai:
PZ a megfigyelő földrajzi szélességének kiegészítő szöge.
ZX a csillag zenit távolsága.
PX a csillag deklinációjának kiegészitő szöge.
A háromszög szögei:
A P pontnál lévő szög H, a csillag óraszöge.
A Z pontnál lévő szög 360 mínusz A, ahol A a csillag azimut
szöge.
Az X pontnál lévő szög q, a parallaktikus szög.
A különböző koordináta-rendszerek gyakorlati felhasználásához olyan összefüggésekre
is szükség van, amelyekkel adott égitest különböző rendszerbeli koordinátáit
egymásba átszámithatjuk.
Ezeket az összefüggéseket a gömbháromszögtan tételei segitségével lehet levezetni.
A csillagászati háromszögre a gömbháromszögtan szinusztételét, valamint az oldalakra és a szögekre vonatkozó koszinusz tételt felirva, a következőket adódnak.
Feltételezve, hogy a megfigyelő szélessége f és a
helyi sziderikus idő (amely szükség esetén a Grenwich-i sziderikus időből és
a megfigyelő szélességéből számítható)
rektaszcenzió (a) és a deklináció (d)
adott, van
Helyi óra szögünk (H = helyi sziderikus idő - rektaszcenzió), órában
A H-t szögre konvertáljuk (15-tel szorozva).
A szélesség j.
Adott H és d, és szeretnénk meghatározni az azimut
(A) és a magasság (a) értékét.
A koszinusz tétel alkalmazásával:
cos(90° - a) = cos(90° - d) cos(90° - j)
+ sin(90° - d) sin(90° - j)
cos(H)
leegyszerűsítve
sin(a) = sin(d) sin(j)
+ cos(d) cos(j) cos(H)
A szinusz tétel alkalmazásával:
sin(360° - A) / sin(90° - d) = sin(H) / sin(90° - a)
leegyszerűsítve
- sin(A) / cos(d) = sin(H) / cos(a)
vagyis
sin(A) = sin(H)cos(d) / cos(a)
Alternatív módon újra alkalmazva a koszinusz tételt:
cos(90° - d) = cos(90° - j)
cos(90° - a)+ sin(90° - j) sin(90° - a) cos(360° -
A)
leegyszerűsítve
sin(d) = sin(j) sin( a) +
cos(j) cos(a) cos(A)
átrendezve
cos(A) = [sin(d) - sin(j)
sin(a)] / cos(j) cos(a)
És az ellenkező problémára:
Ha adott j, a és A, akkor mennyi a
és d?
A koszinus tételt alkalmazva a d kifejezéséhez, a
fentiek szerint:
sin(d) = sin(a) sin(j)
+ cos(a) cos(j) cos(A)
A szinusz tételt használva a H kifejezéséhez, a fenti képlet szerint:
sin(H) = - sin(A) cos(a) / cos(d)
Vagy helyette a koszinus tételt alkalmazva:
sin(a) = sin(d) sin(j) + cos(d)
cos(j) cos(H)
átrendezve
cos(H) = [sin(a) - sin(d) sin(j)]
/ cos(d) cos(j)
A számításban feltételezve, hogy H a helyi sziderikus idő (t).
Akkor a rektaszcenzió adódik a következő összefüggésből:
a = t - H