A fizika legérdekesebb fogalma: a tömeg
Ráállunk az utcai mérlegre. A mérleg kezelője azt mondja
például: "Az ön súlya 63 kilogramm."
Egészen furcsán hangzanék, ha azt mondaná: "Az ön tömege
63 kilogramm."
De ez is helyes kifejezés lenne.
Az előbbi részben a Holdról
azt mondtuk, hogy a tömege 80-szor kisebb, mint a Föld
tömege. Teljesen helytelen
lenne, ha ehelyett azt mondanánk, hogy a Hold
súlya 80-szor kisebb, mint a Föld
súlya.
Az eddigi példáinkban szereplő testekről egyszer azt mondtuk, hogy súlyuk például
ezer kilogramm (10.000 N),
máskor azt mondtuk, hogy tömegük
ezer kilogramm.
Néha ugyanabban a példában felváltva használtuk a súly és a tömeg
kifejezést.
Mi különbség van egy test súlya és tömege
között?
Mikor használunk "tömeg"
szót, és mikor helyes a "súly" kifejezés?
Mit jelent az, ha azt mondjuk, hogy egy rakéta "tömege"
1.000 kilogramm?
Helyesebb-e, ha ezt a rakétát 1.000 kilogramm
tömegünek nevezzük,
vagy az a jobb, ha 1.000 kilogramm (10.000 N)
súlyúnak mondjuk?
Űrhajóra szállunk egy liter vízzel
Mindenki tudja, hogy 1 liter 4 °C hőmérsékletű tiszta víz súlya 1 kilogramm (10 N).
Mi okozza ezt a súlyt?
A testek súlyát az okozza, hogy a test (az egy liter víz) meg a Föld vonzzák
egymást.
Hogyan lehetnek megmérni ennek a vonzóerőnek a nagyságát?
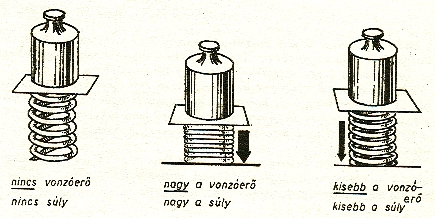
Nagyon egyszerűen. Az egy liter vizet rugóra függesztjük. A rugó megnyúlik.
A testek súlyát rugós erőmérővel mérhetjük, és rugós erőmérővel állapíthatjuk
meg, hogy az egyik test súlya hányszor akkora, mint egy másik test súlya.
De mi történne akkor, azt az egy liter vizet más égitestre vinnénk?
A vonzóerő nagysága, a test súlya más lenne. Két példát már említettünk. A Hold
anyagának mennyisége sokkal kevesebb, mint a Földé. A Hold felületén a vonzóerő
csak hatodrésze a Föld felületén tapasztalt vonzóerőnek. A Nap felületén pedig
28-szor akkora a vonzóerő, mint a Földön.
Ezért az 1 liter víz súlya a Holdon csak 1/6 kilogramm (10/6 N), a Nap felületén
pedig 28 kilogramm (280 N).

A testek súlya a vonzóerő nagyságától függ. A súly a testek nem állandó, nem változatlan tulajdonsága.
Tegyük fel, hogy a Világegyetemben van egy olyan hely, ahol semmiféle
erő nem hat az ott lévő testre. Van-e itt a testnek, az egy liter víznek súlya?
Nincs! Egy gondolatbeli rugósmérleg semennyit sem nyúlna meg, ha ráakasztanánk
az egy liter vizet.
Most már világos, hogy mit jelent a testek "súlya"!
A testek súlyát a tömegvonzás, a gravitáció okozza. Ugyanannak a testnek (pl.
egy liter víznek) a súlya más-más nagyságú lehet a Világegyetem különböző helyein.
Az 1liter víz súlya a Föld felületén 1 kilogramm (10 N), de elképzelhetünk olyan helyet,
ahol ugyanennek az 1 liter víznek a súlya 1.000 vagy 10.000 kilogramm is lehet.
Sőt olyan hely is elképzelhető, ahol egyáltalán nincs súlya.
A súly a testnek, annak az egy liter víznek egyik tulajdonsága. De ez a tulajdonság
nem állandó, hanem helyenként változik. Már említettük, hogy nem kell elmenni
a Hold felületére, mert ha csak egy lépcsőfokkal feljebb lépünk, máris kisebb
lesz a súlyunk, pedig testünk anyagának mennyisége nem változott meg.
A lényeg tehát ez: a testek súlya nem állandó, hanem helyenként változó.
Felmerül a nagy és érdekes kérdés: van-e a testnek valami olyan tulajdonsága,
amely a Világegyetem bármely helyén állandó marad? Van-e ennek az egy liter
víznek olyan tulajdonsága, amely ugyanaz marad akár a Holdra, akár a Napra,
akár a Nap közepében uralkodó 20 millió fokos hőségbe visszük? Ennek a tulajdonságnak
a testre nézve jellemzőnek és jól mérhetőnek kell lennie.
Ez a kérdés valóban érdekes!
Az előbb, amikor a súlyról beszéltünk, az egy liter vizet
rugóra függesztettük és a rugó megnyúlását figyeltük. Ha a rugó jobban megnyúlott
azt mutatta, hogy nagyobb lett az egy liter víz súlya.
Most az egy liter vizet tegyük gondolatban egy súlytalan és súrlódás nélkűl
szabadon mozgó kis kocsira. A kocsit majd rugós erőmérővel kell húzzuk. Az egy
liter vízre, most semmilyen más erő nem hat, csak a húzóerő.
Mi történik, ha az 1 liter vízre, 1 másodpercig 1 kilogramm húzóerőt fejtünk
ki?
Ez a jólismert és sokszor alkalmazott alapesetünk: ha 1 liter (1 kg) vízre,
1 másodpercig 1 kilogrammsúlynyi (10 N) erő hat, akkor az 1 liter víz 10 méter másodpercenkénti
végsebességet ér el.

Ha a világmindenség bármely pontján hat 1 liter vízre 1 másodpercig 1 kilogrammsúlynyi (10 N) erő - annak a víznek a végsebessége mindenütt 10 méter lesz másodpercenként. Tehát az 1 liter víz (vagy bármely test) mindenütt ugyanakkora ellenállást fejt ki a mozgatóerővel szemben (ábra). A testek tömege mindenütt változatlan marad - állandó.
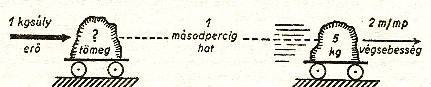
Gyorsítási kísérlettel a Világegyetem bármely részén megtudhatnánk valamely test tömegét, 1 liter víz (1 kg) tömegében kifejezve (ábra).
Mi lesz a végsebesség akkor, ha a kocsira 2, 3 liter vizet teszünk és most
is 1 kg (10 N) súlyerővel húzzuk 1 másodpercig?
Akkor a másodperc végén a végsebesség kétszer, háromszor kisebb lesz. - Mindezt
eddig is tudtuk. Sőt talán még a következő kérdésre is tudnánk felelni:
A kis kocsin ismeretlen mennyiségű víz van. Nem sejtjük, hogy hány liter. De
amikor 1 kg (10 N) erővel 1 másodpercig megtoljuk a kocsit, 2 méter lesz a végsebessége
másodpercenként. Hány liter víz van a kocsin?
Mivel a végsebessége nem 10 méter/másodperc, hanem 5-ször kevesebb, azaz 2 méter/másodperc,
ezért a mozgásba hozott víz 5-ször több mint 1 liter azaz 5 liter víz van a
kocsin.
Bárhol végezzük is el ezeket a gyorsítási kísérleteket,
még a legmagasabb hegy tetején is ugyanarra az eredményre jutunk, mint a tengerszinten.
Ezért bizonyos, hogy a Hold vagy a Nap felszínén is ugyanez lenne a kísérlet
eredménye.
Vagyis: a Világegyetem bármely helyén hat arra az 1 liter vízre 1kgsúly (10 N) erő
1 másodpercig, mindenütt 10 méter másodpercenkénti végsebességet ér el.
Eszerint a testeknek, az anyagnak van olyan tulajdonsága, amely a világmindenség
minden helyén változatlan marad, állandó:
ugyanaz a test a Világegyetem bármely részén ugyanakkora
mértékben áll ellen a mozgását megváltoztató erőnek.
A testeknek a mozgásuk megváltoztatásával szemben tanusított ellenállását
tehetelenségnek nevezzük.
Ezért tapasztalatunkat úgy fejezhetjük ki, hogy: jóllehet ugyanannak a testnek
a súlya a Világegyetem különböző helyein változik, de a testnek a mozgatóerővel
szemben tanusított ellenállása, a test tehetetlensége mindenütt állandó.
Példánkban láttuk, hogy a testek tehetetlenségének nagyságát lemérhetjük. Ha
ugyanakkora erőt alkalmazunk, és az elért végsebesség egy másik esetben kétszer,
háromszor kisebb, akkor annak a másik esetben mozgatott testnek a tehetelensége
kétszer, háromszor nagyobb, mint az első esetben mozgatott test tehetelensége.
Ha egy testnek a mozgatóerővel
szemben tanúsított ellenállása, tehetetlensége
mondjuk százszor akkora, mint egy liter
vízé, akkor azt mondjuk, hogy annak a testnek a tömege
százszor nagyobb, mint egy liter
víz tömege.
Aki az eddigieket jól megértette, meg tudja oldani a
következő feladatot.
Feladat: két vasdarab fekszik előttünk az asztalon, egy kisebb és egy
nagyobb. Hogyan tudnánk megmérni azt, hogy a nagyobbik tömege hányszorosa a
kisebbik tömegének?
Megoldás: ugyanakkora erővel, ugyanannyi ideig gyorsítanánk először az
egyiket, azután a másikat. Ha azt tapasztalnánk, hogy a nagyobbik vasdarab végsebessége
tízszer kisebb, mint a másik vasdarabé, akkor a nagyobbik vasdarab tömege tízszerese
a kisebbik vasdarab tömegének.
Íme anélkül, hogy a testek súlyát ismernénk, meg tudjuk mérni, hogy az egyik
hányszor akkora tömegű mint a másik.
Az előbb két vasdarabról volt szó. Mozgatási kísérlettel
megállapítottuk, hogy az egyiknek az erővel szemben gyakorolt ellenállása, tehetetlensége,
tehetelen tömege tízszer akkora, mint a másiké.
Most következik a meglepő tapasztalat.
Függesszük fel rugós erőmérőre külön-külön mindegyik vasdarabot. Egyszóval mérjük
meg a súlyukat. Azt tapasztaljuk, hogy a tízszer nagyobb tömegű
vasdarab súlya is tízszer nagyobb.
Mi ebben a meglepő?
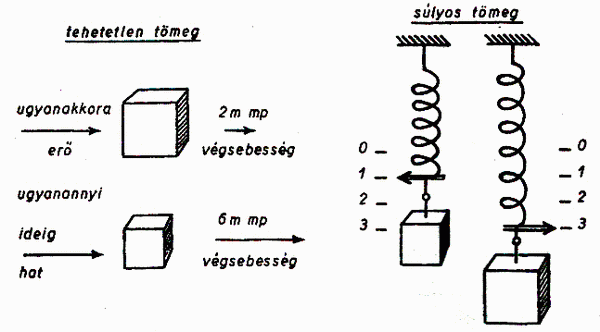
Ha valamely test tehetetlen tömegét
például 3-szor akkorának találjuk, mint a másik testét, akkor annak a testnek
a súlyos tömege
(ami a rugó megnyúlását okozza) is 3-szor akkora, mint a másiké (ábra).
Amikor a vasdarabok
tehetetlenségét, tömegét
mozgatási kísérlettel megállapítottuk, ebben semmi szerepe sem volt a testek
egymásra gyakorolt hatásának, a gravitációnak.
Amikor pedig rugóra felfüggesztettük a vasdarabokat,
nem mozgattuk, csupán a Föld
vonzásának tettük ki őket. Azt tapasztaltuk, hogy amelyik
vasdarab tízszer
jobban ellenáll a gyorsítóerőnek, az a vasdarabot
tízszer jobban vonzza a Föld
is !
Ezt úgy mondjuk, hogy:
ha egy testnek a tehetetlen tömege tízszer akkora, min egy másik testé, akkor annak a testnek a súlya is tízszer akkora (annak a testnek súlyos tömege, gravitációs tömege is tízszer nagyobb). Valamely test tehetetlen tömege ugyanakkora, mint a gravitációs tömege.
Teljesen mindegy tehát, hogy két testnek a mozgatóerővel szemben tanusított
ellenállását, vagyis a tehetetlenségét mérem-e meg, vagy a két testnek a súlyát.
Mindkét mérés alapján megmondhatjuk, hogy az egyik test tömege
hányszor akkora, mint a másik test tömege.
A kétféle mérés végeredménye ugyanaz! Pedig a mozgatással szemben gyakorolt
ellenállás egészen más tulajdonság, mint a tömegvonzás.
Mi lehet ennek a meglepő egyezésnek az oka?
Erre ma még nem tudunk magyarázatot adni. De könnyebb felelni arra a kérdésre,
hogy valóban pontosan ugyanakkorának adódik-e a kétféle módon mért tömeg,
vagy a két érték csak pontatlanul egyezik.
Különféle eljárásokat dolgoztak ki, hogy nagyon pontosan meg tudják mérni egy
test tehetetlen tömegét
és gravitációs tömegét.
Ilyen mérést Eötvös Lóránd is végzett. Megállapította, hogy a kétféle módon
mért tömeg számértéke
kétszázmilliomod-résznyi pontossággal egyezik. A mai, kb. százszor pontosabb
mérések is igazolták a kétféle tömeg
azonosságát.
Mi különbség van egy test tömege és súlya között?
Most már felelni tudunk erre:
a testek tömege változatlan, súlyuk pedig egy másik testtől is függ, amellyel kölcsönösen vonzóhatásban állnak.
Mi helyesebb, az, ha a Föld vagy a Hold súlyáról beszélünk, vagy a tömegükről?
A Föld vagy a Hold
súlyáról beszélni oktalanság.
A Földnek legfeljebb
a Napra és a többi égitestre
nézve lenne megadható súlya.
De még a Napra vonatkoztatott
súlya is folyton változnék,
mert hiszen ha közelebb kerül a Naphoz,
akkor nagyobb a tömegvonzás
ereje, mintha távolabb van. Viszont a Föld,
a Hold tömege
állandó. Az égitesteknek
csak a tömegéről beszélni
értelmes dolog.
Ha a Föld felületén
levő tárgyakról, például egy emberről vagy egy mozdonyról van szó, akkor mindegy,
akár azt mondjuk, hogy az ember súlya
68 kg (680 N), a
mozdonyé 100.000 kg (1.000.000 N), vagy azt mondjuk, hogy a tömegük
68, illetve 100.000 kg.
De ha a Hold (vagy más
égitest) felületén
lévő szikladarab nagyságát akarjuk felismerni, akkor azt kell mondani, hogy
a tömege például 100.000
kg. Ha a szikladarabot a Földre
hoznánk, akkor a súlya
is 100.000 kg (1.000.000 N) lenne. De a Hold
felületén sokkal (hatszor) kisebb a 100.000 kg tömegű
szikladarab súlya.