 Ezt a 100 kgsúly
erőt számítsuk át milligrammsúlyokra.
Ezt a 100 kgsúly
erőt számítsuk át milligrammsúlyokra.Hogyan lehet megtudni a távoli égitestek tömegét?
"Vitézek mi lehet e széles föld felett ..."
időszámításunk előtt 496 évvel született Szofoklész, a legnagyobb görög
tragédiairó. Elámult azon, hogy milyen nagy dolgokra képes az ember: vet, arat,
hajót épít, az állatokat eke elé fogja, a tűz erejével formálja a bronzot. Mindez
annyira megihlette hogy a Földön található dolgok között a legcsodálatosabbnak
az embert nevezte.
Azóta két és fél ezer év múlt el.
Milyen dalt kellene írnia ma, ha látná elektromos erőműveinket, éjszaka is nappali
fényben ragyogó városainkat, a mozit, a televíziót!? Hogy ezek nagyszerűségét
észrevegyük, ahhoz nem kell különös tudomány.
De vannak felfedezések, mérések, eredmények, amelyek nem ilyen feltűnők, de
még csodálatosabbak, még jobban bizonyítják az emberi szellem nagyságát.
Nem tudom, mit szólnánk hozzá, ha azt a megbízást kapnánk, hogy mérjük meg a Föld kerületét vagy határozzuk meg, hogy milyen messzire van a Hold. De mindezt
a saját erőnkből, nem szabad kérdezni senkitől semmit.
Pedig ezeket a méréseket már több mint kétezer évvel ezelőtt elvégezték, meglepő
pontossággal. időszámításunk előtti III. században Eratoszthenész 1%-on
belüli pontossággal megmérte a Földgömb kerületét. A pontos érték 40 008 kilométer.
Az Ő eredménye pedig 39690 kilométer volt.
Ma már tudjuk, hogy a Hold
60 földsugár távolságra van a Földtől.
Kétezer évvel ezelőtt ezt a távolságot 56 földsugárnak mérték. Ez is bámulatunkra
méltó pontosság.
De ha valamelyik ókori tudósnak azt mondták volna hogy eljön az idő, amikor
azt is meg tudjuk majd mérni, hegy hányszor akkora a Föld,
a Nap, vagy a távoli
csillagok tömege,
mint a kezünkben tartott kődarabé (mondjuk egy kilogrammé)
- ezen alighanem elcsodálkozott volna.
Igaz kétezer évnek kellett elmúlnia amíg idáig fejlődött a tudomány. Sok mindenről
hallunk, olvasunk, sok mindent látunk a moziban is. De nem hiszem, hogy ezzel
a kérdéssel már találkoztak volna: hogyan lehet megtudni, hogy hány kilogramm
a Föld, a Hold tömege?
A Föld tömegének megállapítása nagyon egyszerű. Eddigi tudásunk teljesen elegendő
ahhoz, hogy bárki önerejéből kiszámítsa kétperces gondolkodás közben.
Íme, bebizonyítjuk.
Mint mindenkor, most is abból indulunk ki, amit tudunk, és gondolkodással jutunk
el ahhoz, amit eddig nem tudtunk.
Emlékezzünk vissza a tömegvonzásra vonatkozó alapesetre. A Föld tömegét ebből
a tapasztalati tényből számítjuk ki:
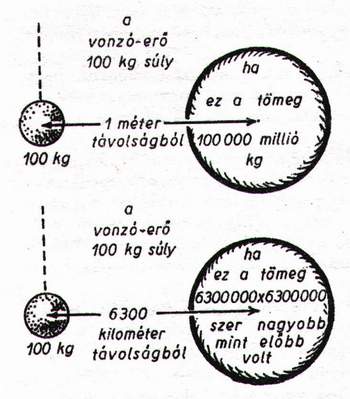
100 kilogrammos gömb egy másik 100 kg-os gömböt 1 méter távolságból kb. 1 tízezred
grammsúly (0,1 milligrammsúly) erővel vonz.
Ámde az ismeretlen tömegű Földgömb azt a 100 kilogrammos gömböt nem tízezred
gramm, hanem 100 kilogrammsúly erővel vonzza. Ebből ki lehet következtetni,
hogy mekkorának kell lennie a Föld tömegének, hogy kifejthesse a 100 kgsúly
vonzóerőt (ábra).
Induljunk el az egyszerű következtetés útján.
1. Először is számítsuk ki azt, hogy mekkora tömeget kellene attól a 100 kg-os
golyótól 1 méter távolságra helyezni, hogy a vonzóerő 100 kilogrammsúly legyen.
 Ezt a 100 kgsúly
erőt számítsuk át milligrammsúlyokra.
Ezt a 100 kgsúly
erőt számítsuk át milligrammsúlyokra.
100kg = 100.000 gramm = 100.000.000 milligramm.
Ha a 100 kg-os golyót 1 méter távolságból egy másik 100 kg-os golyó vonzza,
akkor a vonzóerő 0,1
milligramm. De mi azt akar juk, hogy a vonzóerő
100.000.000 milligramm legyen. Ezt az 1000 milliószor nagyobb vonzóerőt
1 méter távolságból 1000 milliószor nagyobb tömeg
fejti ki. Tehát a keresett tömeg
1000 milliószor 100 kg = 100.000 millió kg.
Kérdésünkre tehát ez a felelet:
a 100kg tömegű golyótól
1 méter távolságra egy másik de 100.000 millió kilogramm
tömegű golyót kellene
elhelyezni, hogy 100 kgsúly erővel
vonzzák egymást.
A Föld tömegét úgy tudjuk meg, hogy kiszámítjuk azt a tömeget, amely 100 kg-ot 100 kgsúly erővel vonz földsugámyi távolságból.
2. De a mi esetünkben ez a másik gömb a Földgömb.
A Földgömb úgy vonz,
mintha egész tömege
a középpontjában volna egyesítve.
Tehát az a 100 kgsúlynyi vonzást kifejtő golyó középpontja nem 1 méternyire
kell hogy legyen az első golyótól hanem olyan messzire, mint a Föld
sugara, kereken 6.300 kilométerre, 6.300.000 méternyire.
Azt a második vonzó tömeget
tehát nem 1 méternyire kell elhelyezni az első tömegtől,
hanem 6.300.000 méternyire, de úgy, hogy a vonzóerő
nagysága változatlan maradjon.
Tudjuk, hogy ha azt akarjuk, hogy a vonzóerő
változatlan maradjon, akkor 2-szer, 3-szor nagyobb távolságban 4-szer, 9-szer
nagyobb tömegnek kell
hatnia.
A mi esetünkben a távolság 1 méter helyett 6.300.000 méter lett. Ezért, hogy
mégis megmaradjon az a 100 kilogrammsúlynyi (1000 N) vonzóerő,
6.300.000 . 6.300.000-szer akkora tömegnek
kell hatnia, mint amennyit előbb kiszámítottunk.
Az előbbi lépés végén kiszámított tömeg
100.000 millió kg. Ezt még meg kell szorozni 6.300.000-rel. Az eredményt újra
meg kell szorozni 6.300.000-rel. Akkor megtudjuk a Föld
tömegét kilogrammokban.
Tehát a Föld tömege
100.000.000.000 . 6.300.000 . 6.300.000
kg = 3.969.000.000.000.000.000.000.000 kg,
kereken 4.000.000.000.000.000.000.000.000 kg.
Szóval a Föld tömegét
kilogrammokban számításunk
szerint olyan szám fejezi ki, amely 4-gyel kezdődik, és utána 24 zérus következik,
vagyis 25 jegyű szám.
Ez teljesen elegendő ahhoz, hogy tájékoztasson bennünket a Föld
tömegének nagyságáról.
Ha pontosabb adatokat használnánk, akkor a pontosabb eredmény szerint a 24 zérus
előtt nem a 4-es számjegy állna, hanem a 6-os.
A Föld tömege
pontosabban
Mekkora a Föld átlagos sűrűsége
Az előbbi szám egyszerűen elképzelhetetlen számunkra. De azonnal igen elképzelhető és hasznos összehasonlító adathoz jutunk, ha ezt a számot elosztjuk a Földgömb literekben kifejezhető köbtartalmával. Akkor megtudjuk azt, hogyha a Földet szépen szétmorzsolnánk egyenletes sűrűségre, és ebből az anyagból egy Iiternyit felmerítenénk, az hány kilogramm lenne.
Ha a számítást valóban elvégeznénk, azt találnánk hogy a Földgömb összemorzsolt
anyagából 1 liternyinek a tömege 5,5 kg. Tehát
a Föld anyagából 1 liter átlagosan 5,5 kilogrammot nyom.
De 1 liter víz súlya 1 kilogramm.
Ezért a Föld anyagának átlagos fajsúlya (és sűrűsége is) majdnem
6-szor akkora, mint a vízé.
A vas sűrűsége
körülbel 8. Mivel a Föld
felszínét alkotó anyagok, a kövek, a talaj átlagos sűrűsége
csak kb. 2,5 - 3, ezért a Föld
belsejében jóval sűrűbb anyagoknak kell lenniök, hogy kiadódjék az átlagos 5,5
sűrűség.
Mekkora a többi égitest tömege?
A Föld ás a többi égitest tömegét aligha célszerű kilogrammokban vagy tonnákban
mérni, mert olyan roppant nagy számokhoz jutunk, amelyek elveszítik szemléletességüket.
Ezért egyszerűen a Föld tömegét egységnek tekintjük, ás hozzá hasonIítjuk a
többi égitestnek, például a Napnak, a Holdnak a tömegét.
A Nap tömege 333 000-szer akkora, mint a Föld tömege.
A Mars bolygó tömege a Föld tömegének kilenced része.
A Hold tömege 81-szer kisebb, mint a Föld tömege.
A Föld tömegét aránylag egyszerű módon tudtuk kiszámítani.
De hogyan lehet megtudni a Nap tömegét?
Ugyanúgy, mint ahogyan a Föld tömegét kiszámítottuk. Gondoljuk át röviden hogy
milyen utat követtünk, hogy ezt alkalmazhassuk a Napra is.
A Föld tömegének kiszámításakor
a tömegvonzásra vonatkozó alapesetünkből indultunk kí. Csak azt kellett kikövetkeztetni,
hogy mekkora tömeget kell a Föld
középpontjába képzelni, hogy ez a tömeg 6.300 kilométer távolságból 100 kgsúlynyi
erőt gyakoroljon a (Föld felszínén levő) 100 kg tömegre.
Tudjuk, hogy a Nap 150 millió kilométernyire van a Földtől. Ha valaki megmondaná
nekünk azt, hogy a Nap mekkora erővel vonzza a Föld távolságában levő 100 kg-os
testet, akkor a számítást ugyanúgy végezhetnénk, mint előbb. Alapesetünkből
kiindulva következtetnénk arra, hogy 150 millió kilométer távolságban mekkora
tömegnek kell lennie, hogy ekkora vonzóerővel hasson.
De ki súgja meg nekünk azt, hogy a Nap mekkora erővel vonzza a tőle 150 millió
kilométerre levő 100 kilogrammos testet?
Magunk is könnyen kitalálhatjuk.
A Nap akkora erővel vonzza azt a testet, mint amekkora erővel arra a testre
a Nap körüli keringéséből eredő röpítőerő hat.
Ámde ennek a röpítőerőnek a nagyságát már ki tudjuk számítani, hiszen mindent
ismerünk, ami szükséges. Ismerjük a pálya sugarát
(150 millió km), ismerjük egy körülforgás idejét a Nap körül: 365 nap.
- Ki tudjuk tehát számítani azt, hogy ha 150 millió kilométer hosszú zsineg
végére 100kg-os testet kötnénk és 365 nap (kb. 30 millió másodperc)
alatt egyszer körülforgatnánk, mekkora röpítőerő
hatna rá (alapeset a körmozgásnál).
Ekkora erővel vonzza a Nap a Föld távolságában levő 100kg-os testet. Most már
az említett módon kiszámítható Nap tömege.
Mekkora a Nap átlagos sűrűsége?
Ha a Nap tömegét elosztunk a Nap köbtartalmával, akkor megtudjuk a Nap sűrűségét.
Mi az eredmény? Sűrűbb anyagból áll-e a Nap, mint a Föld? A számítás szerint
a Nap anyagából 1 liter tömeg 1,4 kg. Ha tehát
1 liternyi Nap-anyagot a Földre hoznánk, itt 1,4 kg lenne a súlya.
A Nap anyaga átlagosan másfélszer olyan sűrű, mint a víz, és fele olyan
sűrű, mint az alumínium. A Nap anyagának átlagos sűrűsége körülbelül akkora,
mint a kokszé.
És a többi égitest sűrűsége?
A Hold közepes sűrűsége 3,3. Ritkább anyagokból áll, mint a Föld. A Naphoz
legközelebb keringő Merkur nevű bolygó sűrűsége (5,3)
majdnem pontosan annyi, mint a Földé (5,5).
A Szaturnusz áll a legritkább anyagból, mert közepes sűrűsége (0,7) még
a víznél is kisebb, körülbelül olyan sűrű, mint a petróleum.
Melyik bolygó tömeg a legnagyobb?
A Jupiteré, 318-szor akkora, mint a Föld tömege, de a Jupiter sűrűsége
csak negyedrésze a Föld sűrűségének.
Mindez valóban elismerésre méltó eredménye a tudománynak. Naprendszerünkön
kívül vannak olyan csillagok, amelyek anyagának átlagos sűrűsége több tízezerszer
akkora, mint a Földé.
Mennyire pontosak az ilyen adatok?
Ha a boltban 1 kilogramm
cukrot veszünk, és az eladó ezt 1% pontossággal méri le, az 1 dekagramm hibával
meg vagyunk elégedve. - Vajon a bolygók tömegét
meg tudjuk-e mérni olyan pontosan, mint üzletben az árut, mondjuk 1%-os pontossággal?
A Jupiter tömegét
a körülötte keringő holdak
távolságának és keringésidejének ismerete alapján olyan pontosan lehetett kiszámítani,
mintha az üzletben 1 kg cukrot csak 1 tizedgramm eltéréssel mérnének le. Ez
százszor pontosabb, mint amit említettünk.
De még meglepőbb példát is mondhatunk. Az égitestek tömegének
kiszámítására többféle módszer van. Például az egyik bolygó
a másikra vonzást gyakorol. Ha keringésük közben egymás közelébe kerülnek, megzavarják
egymás pályáját. Ezt
megfigyelik a csillagászok. A zavarás annál nagyobb, mennél nagyobb a zavaró
bolygó tömege és mennél
kisebb a megzavart bolygó tömege.
A Jupiter tömegét annak alapján is kiszámították, hogy mennyire zavarta meg
a közelében elhaladó üstökösök pályáját. Ily módon olyan pontosan lehet megállapítani
a Jupiter tömegét, mintha egy kilogramm cukrot a gramm századrésznyi pontosságával
mérnénk le.
Ekkora pontossággal mérték meg a Jupiter bolygó tömegét Is.
|
Miből számították
|
Ha ilyen pontosan mérnénk meg 1 kg-ot a hiba ennyi milligram
lenne
|
|
| A Szaturnusz bolygó pályájának megzavarásából |
1047,877
|
120
|
| A Jupiter egyik holdjának mozgásából |
1047,49
|
60
|
| Egy üstökösre gyakorolt zavaró hatásából |
1047,35
|
40
|
| Egy másik üstökös pályájának megzavarásából |
1047,176
|
10
|
Tehát a csillagászok pontosabban mérik a távoli bolygók tömegét, mint amilyen pontosan a gyógyszerész mér a patikai mérlegen.
A többi csillagnaphoz képest kicsi vagy nagy a Nap tömege?
Ki tudjuk-e számítani a bolygórendszerünkön kívül eső távoli csillagok
tömegét is? Olyan csillagokét,
ahová a fény is csak
évek múlva ár el?
Ezek között a csillagok
között sok úgynevezett kettöscsillag
van, amelyek egymás körül keringenek. Ha ismerjük a közöttük levő távolságot
és a keringésidőt, kiszámítható az égitest
tömege.
Mekkora tömegű csillagokat
találtak?
Rajzoljunk egy gömböt akkora sugárral, amit a fény
30 év alatt fut be. Ezen a gömbön belül megvizsgált 200 kettőscsillag
közül kb. 63%-nak a tömege
körülbelül akkora volt, mint a Napunké.
A csillagok 3%-ának
tömege a Nap
tömegének kétszerese
és tízszerese között volt. A csillagok
34%-ának tömege kisebb
volt.
Napunk tehát a normális tömegű
csillagok közé tartozik.
Az elmondottakból láthatjuk, hogy milyen fontos az égitestek
mozgásában a tömegvonzás
és a kör kerületén történő mozgás ismerete, és az a tény, hogy a röpítőerő
nagysága egyenlő a vonzóerővel.
Ezek alapján ki tudtuk számítani az égitestek
tömegét.
Ha pedig ezenfelül a csillagászok távcső
segítségével megmérik az illető égitestek
sugarát, akkor kiszámíthatjuk térfogatukat és sűrűségüket
is.
Ezzel átjutottunk a fizika legtöbb gondolkodást
kívánó területein. Néha alapos szellemi munkát kellett végezni, hagy az átértett
tudás csúcsaira feljuthassunk. De megérte!
Ezentúl könnyebb dolgunk lesz. Ezt bizonyítja a következő fejezet, amelyből
megtudjuk, hogy a gép százszor olcsóbban is dolgozhat, mint az izomerő.