Kiszámítjuk, hogy mekkora sebességet kell adni az űrrakétának, hogy örökre elhagyja a Földet
avagy
miért nincs légköre a Holdnak?

 

A rakéta szökési sebessége és a gázmolekulák

Már eddig is sok érdekes kérdést beszéltünk meg. Nehéz lenne eldönteni, hogy melyik volt szebb, nagyobb. De ha az olvasók figyelemmel kísérik ezt a fejezetet, alighanem sokan szavaznának arra, hogy ez a legérdekesebb. Most olyan kérdésekről lesz szó, amelyek foglalkoztatják a képzeletet és szeretnénk jobban megismerni őket.
Így például ma már az érdeklődő gyermek is tudja, hogy ha az űrrakétát 11,2 km másodpercenkénti sebességgel lőjük ki, akkor örökre elhagyja a Földet. Ez az úgynevezett szökési sebesség.
De azt aligha tudja, hogy miért kell éppen 11,2 kilométer másodpercenkénti sebességet adni annak a rakétának? Hogyan jöttek rá erre? Hogyan lehetett kiszámítani?
Alighanem elismeréssel néznénk arra, aki ceruzával kezében ki tudná számítani ezt a szökési sebességet. Pedig a fejezet elolvasása után bármelyikünk meg tudja majd tenni. Ez lesz egyik feladatunk.
De van egy másik kérdés is, amely legalább ennyire érdekes: miért nincs a Holdnak légköre?
Miért van a Földnek légköre?
Miért van a Jupiternek igen sűrű légköre? Miért fizikai lehetetlenség, hogy a Holdnak és az úgynevezett kisbolygóknak légköre legyen?
Örökre megmarad-e a Föld légköre, vagy elvesztheti valaha?
Érdekes kérdések. Eddigi tudásunk alapján már felelni tudunk rájuk.
De egyáltalában, milyen összefüggésben van a bolygók légköre az űrrakétával?
Az összefüggés roppant egyszerű. Ugye az űrrakéta megszökik a Földről, ha 11,2 kilométer másodpercenkénti sebességgel lőjük ki. Nos, a bolygók légkörét alkotó gázok molekuláinak mindegyike egy-egy ilyen rakétának tekinthető. A gázmolekulák megszöknek a Földről, megszökhetnek a többi égitestről is, ha elég nagy sebességre tesznek szert.
A természet már régen sikerrel megalkotta az űrrakétákat: a Holdról is, a kisbolygókról is kilődözte a légkör alkotására hivatott gázok molekuláit, atomjait.
Az összefüggések valóban megint izgalmasak kezdenek lenni, főleg ha a hintát is bekapcsoljuk meggondolásainkba. Az űrrakéta, a szökési sebesség, a légkör megmaradásának kérdésében milyen szerepe lehet a hintának?
Azonnal meglátjuk. Valami ismertből kell kiindulnunk. Űrrakétán még senki sem ült, de hintán igen! Előbb éppen a hintáról esett szó. Folytassuk ezt, és meglátjuk, hogy milyen egyszerűen oldódik meg az a kérdés, hogy mikor szökhetik meg egy bolygóról a rakéta vagy a gázmolekula.

 

A hinta, a személyvonat és egy új alapeset

Mekkora sebességgel halad a hinta, amikor a legalsó helyzetén átsuhan. Haladhat-e ilyenkor a hintázó olyan sebesen, mint a személyvonat?
Egy kis gondolkodással bárki meg tudna felelni erre a kérdésre is.
Már néhányszor említettük, hogyha a személyvonat 36 kilométer óránkénti sebességgel halad, akkor másodpercenként 10 méter utat tesz meg.
A hintának tehát a legalsó helyzetében 10 méter másodpercenkénti sebességet kell elérnie. Akkor halad olyan sebesen, mint a személyvonat. Mármost az a kérdés, hogy milyen magasról kell azt a hintát elengedni, hogy 10 méter másodpercenkénti sebessége legyen a legalsó helyzetében?
Példáinkban előfordult már az, hogy ha egy test 5 méter magasról szabadon esik, 10 méter másodpercenkénti végsebességet ér el.
Ezért az 5 méter magasról elinduló hinta a személyvonat sebességével halad át a legalsó helyzetén, és a másik oldalon megint 5 méter magasra emelkedik, ugyanolyan magasra, mint ahonnét elengedtük.
Ebből a jó példából jegyezzük meg azt, amire a következőkben igen nagy szükségünk lesz: ha egy test 10 méter másodpercenkénti sebességgel halad, akkor annyi munkavégző képesség (mozgási energia) van benne, hogy 5 méter magasra tud felemelkedni,
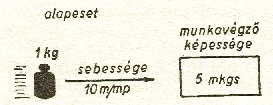
Alkalmazzuk ezt például az 1 kilogramm tömegű testre:

ha az 1 kilogrammos test 10 méter másodpercenkénti sebességgel halad, akkor 5 méterkilogrammsúly munkavégző képesség van benne. Mozgási energiája 5 méterkilogrammsúly (ábra).

Ha bármely test 10 méter másodpercenkénti sebességgel halad, akkor minden kilogramjában annyi mozgási energia van, hogy 5 kilogramsúlyt tudna 1 méter magasra emelni.

Íme, ezt tanultuk a hintától. Most már csak egy lépés az űrrakéta. Ha egy 100 tonnás rakétát csak 5 méter magasra akarunk fellőni, mekkora sebességet kell neki adni?
A felelet könnyű: 10 méter másodpercenkénti sebességet kell adni a rakétának. Teljesen mellékes az, hogy mekkora a rakéta tömege. Mert az alapeset szerint bármilyen rakétának minden kilogrammnyi tömegében annyi munkavégző képesség lesz, hogy éppen 5 méter magasra emeli.
De mekkora sebességet kellene adni a rakétának, ha azt akarnánk, hogy a végtelenbe távozzék?
Akkora sebességet, hogy a rakéta el tudja végezni azt a munkát, ami a végtelenbe emelkedéséhez szükséges.
Ha valaki megmondaná nekünk ezt a munkát, akkor alapesetünkből kiindulva ki tudnánk számítani a szükséges sebességet.
Ennek a munkának a nagysága 6,2 millió mkgs, ha a test tömege 1 kg.

 

Kiszámítjuk a szökési sebességet

Előlegezzük az előbbi adatot. Ha tehát azt az 1 kilogramm tömegű testet úgy akarjuk kilőni az űrbe, hogy a Föld vonzását legyőzve örökre elszakadjon tőlünk, akkora sebességet kell neki adni, hogy kereken 6 millió méterkilogrammsúly energia halmozódjék fel benne.
Mekkora sebességet kell adni az 1 kilogramm tömegnek, hogy munkavégző képessége 6 millió méterkilogramm legyen?
Alapesetünkből kiindulva számíthatjuk ki. Alapesetünk 10 méter másodpercenkénti sebességre szól. A rakétának majd sokkal nagyobb sebességet kell adnunk. Ezért tudnunk kell még azt is, hogy ha a test sebessége kétszer, háromszor nagyobb lesz, akkor hányszor nagyobb lesz a munkavégző képessége, energiája.
A tapasztalat szerint:

ha egy test sebessége 2-szer, 3-szor nagyobb lesz, mint volt, akkor munkavégző képessége 2 . 2 = 4-szer, illetve 3 . 3 = 9-szer akkora lesz, mint volt.

Alapesetünk szerint, ha 10 méter másodpercenkénti sebességgel halad az 1 kilogramm tömegű test, akkor 5 méterkilogrammsúly munkavégző képesség rejlik benne. De mi azt akarjuk, hogy annak az 1 kilogrammos testnek munkavégző képessége 6 millió méterkilogrammsúly legyen.
Próbáljuk meg a sebességet 1000-szer nagyobbra venni. Tehát 10 méter helyett legyen 1000-szer nagyobb sebesség, azaz 10 000 méter, tehát 10 kilométer másodpercenként. Ekkor a munkavégző képesség

1000 . 1000 = 1 000 000-szer nagyobb.

De előbb 5 méterkilogrammsúly volt, most pedig milliószor több lesz, azaz 5 millió méterkilogrammsúly. Ez majdnem annyi, mint a szükséges 6 millió méterkilogrammsúly.
Ha tehát az 1 kilogramm tömegnek 10 kilométer másodpercenkénti sebességet adunk, akkor 5 millió méterkilogrammsúly munkavégző képesség van benne, majdnem annyi, amennyi a szökéshez elegendő.
Még csak egy kicsit kell növelni a sebességet 10 kilométerről 11,2 km-re másodpercenként. Ebben az esetben a munkavégző képesség 1,12 . 1,12 kb. 1,25-szor lesz nagyobb, mint 5 millió méterkilogrammsúly. Az akárhány kilogramm tömegű rakéta tehát örökre elhagyja a Földet, ha sebessége 11,2 km másodpercenként. (ábra).

Ha egy test sebessége másodpercenként 11,2 kilométer, akkor a mozgási energiája elegendő ahhoz, hogy megszökjék a Földről.

Számításunk szép volt, egyszerű volt, mert megmondtuk, hogy az 1 kg-os testnek 6 millió méterkilogrammsúly munkát kell végeznie a nehézségi erővel szemben, ha a végtelenbe távozik.
De honnan tudjuk ezt? Ezt is ki lehet számítani. A számítás módja egyszerű, könnyen megérthető.

 

Mekkora munkát végzünk, miközben az 1 kg tömegű testet a végtelenbe emeljük?

Először csak 1000 kilométernyire vigyük fel azt az 1 kilogramm tömeget a Földtől. Mekkora munkát kell végezni?
1000 kilométer az (1000 . 1000 méter) 1 millió méter. Ha 1 kilogrammot 1 millió méter magasra emelünk, akkor 1 millió méterkilogrammsúly munkát végeznénk - ha annak az 1 kilogramm tömegnek a súlya állandóan 1 kilogrammsúly maradna. De tudjuk, hogy mennél magasabbra emelkedünk, annál kisebb a súly.
Bárki azt is ki tudná számítani, hogy 1000 kilométer magasban az 1 kilogramm körülbelül 3/4 kilogrammot nyom.
Ha evvel a 3/4 kilogrammsúllyal végeznénk a számítást az 1000 kilométeres úton át, akkor az 1 millió méterkilogrammsúly munkának 3/4 része, 750 000 méterkilogrammsúly munkavégzés jönne ki.
A valódi munkavégzés 750 000-nél több, 1 milliónál kevesebb, de meghatározott értéke van (860 000 mkgs, ábra).

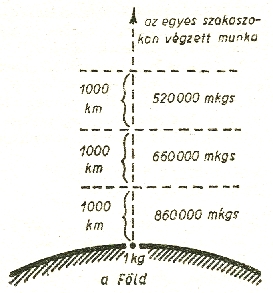Az 1 kilogrammot 1000 kilométerenként egyre távolabb visszük a Földtől. Mennél messzebbre jutunk, annál kisebb munkát kell végeznünk az egymás után következő 1000 kilométeres szakaszokon.

Távolodjunk megint 1000 kilométerrel tovább. Akkor ezen a szakaszon végzett munka jóval kevesebb lesz, mint 750 000 méterkilogrammsúly, a következő 1000 kilométeres szakaszon még kevesebb, és így tovább a végtelenségig. A Földtől nagyon messzire majdnem nulla az egyes szakaszokon végzett munka. mert ott a Föld vonzóereje is roppant csekély.
A valóságban ezt a számítást nem 1000 kilométeres, hanem sokkal kisebb szakaszokra nézve végzik el. A lényeg az, hogy ezek a munkák kiszámíthatók, és ha az egyes szakaszokon végzett munkákat összeadjuk, egy véges számot kapunk.
Ha 1 kilogrammot a Föld felszínéről a végtelenbe vinnénk, körülbelül 6 millió méterkilogrammsúly munkát kellene végezni.
Ha tehát 1 kilogramm tömegű testet a világűrbe akarunk kilőni, akkora sebességet kell neki adni, hogy 6 millió méterkilogrammsúly munkavégző képesség, 6 millió méterkilogrammsúly mozgási energia halmozódjék fel benne.
Ez alig elképzelhető nagy munka. Ha 3 percenként egy-egy 80 kg súlyú zsákot vinnénk fel az 5 méter magas padlásra napi 8 órán keresztül szakadatlanul, akkor 4 hónapig kellene ebben az iramban dolgoznunk, hogy 6 millió méterkilogrammsúly munkát végezzünk.

 

A szökési sebesség a többi égitesten

Nemcsak el akarunk jutni a Holdra ás a többi égitestre, hanem vissza is akarunk róluk térni, kell tehát tudnunk azt, hogy mekkora sebességgel szökhetünk meg róluk.
A Földre vonatkozó számításból látható, hogy a szökési sebesség attól függ, hogy mekkora munkát kell végezni az illető égitest vonzásával szemben, Ha egy bolygón a vonzóerő kisebb, a munka is kisebb, a rakétának kisebb sebességet kell adni, hogy megszökhessék a bolygóról.
A Hold felületén a vonzóerő hatszor kisebb, mint a Föld felületén. Ezért a szökéshez szükséges munka is hatszor kisebb. A rakéta sebességének tehát sokkal kisebbnek kell lennie, mint a Földön.
Valóban, a Holdon a szökési sebesség csak 2,4 kilométer másodpercenként a Földi 11,2 kilométer helyett. Ez nagyon megkönnyíti majd azt, hogy a holdrakéta a Holdról visszatérjen a Földre. - De a Jupiter felületét nem lesz ajánlatos megközelíteni, mert arról a bolygóról a szökési sebesség kb. 60 kilométer másodpercenként.

 

A szökési sebesség és a bolygók légköre

Most már egyszerű meglátnunk az összefüggést.
A gázok legkisebb részecskéi, az atomok és a molekulák nagy sebességgel röpködnek. Így például a 100°C hőmérsékletű hidrogéngáz molekuláinak sebessége 2,2 km másodpercenként. (A hőmérsékletet mindenütt Celsius fokokban adjuk meg, hacsak külön jelölés nincs.) Ha mármost egy bolygó felületén akkora a szökési sebesség, mint amekkora sebességet elérhet az illető bolygón szóbajöhető gázrészecske, akkor azok a gázmolekulák, mint parányi űrrakéták, megszöknek a bolygóról. A bolygó elveszíti légkörét, még ha volt is légköre a bolygó keletkezésekor.
A Holdon a szökési sebesség 2,4 km másodpercenként. A legkönnyebb gáz, a hidrogén molekulájának sebessége pedig csak 2,2 km/mp, kisebb, mint a szökési sebesség. Eszerint a Holdnak lehetne légköre még a legkönnyebb gázból, a hidrogénből is.
Csakhogy valamit nem vettünk figyelembe. Azt, hogy az a 2,2 km/mp a molekulák átlagos sebessége. Ez annyit jelent, hogy ennél többszörösen sebesebb molekulák is akadnak a gázban. Ezek megszöknek. - A gáz felmelegedése közben a kisebb sebességű molekulák is megkapják ezt a nagyobb sebességet, ezért lassanként megszökik az egész légkör.
Még ha a Földről vinnénk is levegőt a Holdra, a gázmolekulák pillanatok alatt elhagynák a Holdat annak napsütötte felén, ahol 135° a hőmérséklet. Ezért a Holdnak nem lehet légköre.
A szökési sebességet kritikus sebességnek is szokás nevezni.
Földünk légköréből is szöknek molekulák a világűrbe?
Igen! A legkönnyebb gázoknak, a hidrogénnek és a héliumnak legsebesebb molekulái kiszöknek légkörünkből. (1 000 000 cm3 levegőben 100 cm3 hidrogén és 4 cm3 hélium van.) De ez a veszteség lényegtelen, és állandóan pótlódik más folyamatokból (pl. a Napból érkeznek hidrogén atommagok).


Felhasznált irodalom