Fajsúly és sűrűség
Nem mind arany, ami fénylik
A réz meg az arany hasonló színű. Ezért anyagukat illetően könnyen össze lehet
téveszteni az ékszereket, ha csak színük alapján ítélünk. Előttünk van két azonos
alakú és színű gyűrű. Hogyan lehet megállapítani, hogy melyik gyűrű arany, melyik
réz. Vagy esetleg a gyűrű csak aranyozott réz, esetleg ezüst!
Ismerősöm egy töltőtollhegyről szerette volna megtudni, hogy arany-e
vagy csak aranyozott.
Elvitte az ékszerészhez. Az kissé megreszelte a toll tompa végét, hogy az esetleges
aranyozást eltávolítsa.
Aztán egy kemény kövön végighúzta a toll megreszelt felületét. A kövön aranyszínű
nyom maradt. Ezután ecsettel folyadékot,
választóvizet vitt
a nyomra. A nyom eltűnt, feloldotta a választóvíz. Ha aranyból
lett volna a nyom, nem oldódott volna fel. A toll tehát csak aranyozott
volt, nem pedig arany.
De mi nem akarjuk megreszelni a gyűrűnket, választóvizünk
sincs. Ezért olyan egyszerű módszerrel ismerkedünk meg, amellyel bárki odahaza
is elvégezheti a vizsgálatot.
Amit jó tudni
1 cm3 víz
súlya 1 gramm. (A gramm a tömeg SI mértékegysége)
De azt már kevesen tudják, hogy 1 cm3 arany
súlya 19,3 gramm. Hogy könnyen megjegyezhessük, tekintsük "egy híján húsznak",
19 grammnak az 1 cm3 arany
súlyát.
Az arany tehát 19-szer súlyosabb, mint az ugyanakkora térfogatú víz. Ezt úgy
mondjuk, hogy az arany fajsúlya 19. De Úgy is mondhatjuk, hogy az arany 19-szer
sűrűbb, mint a víz, vagy az arany sűrűsége a vízre vonatkoztatva 19.
1 cm3 réz súlya pedig 8 - 9-szer akkora, mint 1 cm3 víz súlya. A réz fajsúlya
és sűrűsége a vízre vonatkoztatva 8 - 9.
Az ezüst és az alumínium színe is hasonlít egymáshoz, pedig fajsúlyban, sűrűségben
nagyon különböznek egymástól.
Az alumínium 2,7-szer, az ezüst pedig 10,5-szer (kereken 11-szer) súlyosabb,
mint az ugyanakkora térfogatú víz. Ha ezt tudjuk, akkor azonnal meg tudjuk mondani,
hogy két azonos alakú gyűrű közül melyik az alumínium és melyik az ezüst, ha
színük ugyanaz is. Az ezüst majdnem 3-szor nehezebb, mint az alumínium.
Az aranytárgy pedig több mint kétszer nehezebb, mint az ugyanakkora réztárgy.
Hogyan mérünk fajsúlyt?
Ha ismernénk a gyűrű fajsúlyát,
könnyű dolgunk lenne. Ha a gyűrű fajsúlya
19, akkor bizonyos, hogy tiszta aranyból
van. Ha 8 - 9 a fajsúlya,
akkor tiszta rézből készült,
esetleg aranyozva van
a felülete. Ha pedig 14 - 15 - 17-nek találjuk a fajsúlyát,
azaz egyre közelebb áll a tiszta arany
fajsúlyához, akkor
az a tárgy egyre finomabb aranyötvözetből
készült.
Mekkora egy tárgy fajsúlya akkor, ha 50% az aranytartalma?
 Tegyük fel, hegy egy gyűrű anyaga ezüst és arany ötvözete. Ha a gyűrű fajsúlya
14, akkor a gyűrű súlyának felét arany alkotja. De ha a gyűrű fajsúlya több
mint 14, akkor 50%-nál több benne az aranytartalom. Ha pedig a gyűrű fajsúlya
ennél kisebb, akkor 50%-nál kevesebb arany van benne.
Tegyük fel, hegy egy gyűrű anyaga ezüst és arany ötvözete. Ha a gyűrű fajsúlya
14, akkor a gyűrű súlyának felét arany alkotja. De ha a gyűrű fajsúlya több
mint 14, akkor 50%-nál több benne az aranytartalom. Ha pedig a gyűrű fajsúlya
ennél kisebb, akkor 50%-nál kevesebb arany van benne.
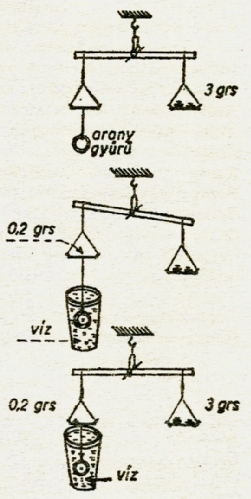
Így mérjük meg a gyűrű fajsúlyát
Ezért nagyon érdekes lesz megtanulni azt, hogy hogyan mérhetjük meg a tárgyak
fajsúlyát. Egy gyűrű
fajsúlyát így határozzuk
meg (ábra):
1. Mérlegen pontosan megmérjük a gyűrű súlyát. Például azt találjuk, hogy a
gyűrű súlya 3 gramm.
2. Most azt kell megtudnunk, hogy mennyi a gyűrűvel egyenlő térfogatú víz
súlya. Ezért a gyűrűt vékony cérnaszálra kötjük és a mérlegen egyensúlyozzuk.
Ezután a cérnaszálon függő gyűrű alá vizespoharat teszünk, hogy a gyűrű a vízben
elmerüljön. A mérleg gyűrűs karja most felemelkedik, mert a gyűrű a vízben
veszített súlyából, mégpedig éppen annyit veszített, amennyi a gyűrű által kiszorított
víz súlya.
A felemelkedett mérlegkar serpenyőjébe súlyokat rakunk, hogy az egyensúly helyreálljon.
Tegyük fel, hogy 0,2 grammot kellett rátenni. Ennyivel lett könnyebb a vízbemerült
gyűrű, ezért a gyűrűvel egyenlő térfogatú víz
súlya 0,2 gramm.
A gyűrű súlyát, a 3 grammot, el kell osztani a 0,2 grammal, akkor megtudjuk,
hogy a gyűrű anyaga hányszor súlyosabb a víznél.
A gyűrű fajsúlya
3 : 0,2 = 15.
Mivel fajsúlya felette
van a 14-nek, az 50%-os aranytartalmú
ötvözet fajsúlyának,
azért a gyűrű 50%-osnál kissé finomabb aranyból
készült.
Foglaljuk össze röviden a mérést: először meg kell mérni a tárgy súlyát a levegőben.
Azután a tárgyat vízbe
lógatjuk és megmérjük a súlyveszteséget. Ha a tárgy súlyát elosztjuk a súlyveszteséggel,
a kapott szám lesz a tárgy fajsúlya.
A fajsúlyból következtethetünk
a tárgy anyagára.
A legnehezebb anyagnak,
az ozmiumnak fajsúlya
22,5, tehát nem sokkal több, mint az aranyé.
A gázok fajsúlya,
így sűrűsége is mintegy
1000-szer kisebb a vízénél.
Néhány anyag fajsúlya
(1 cm3 anyag súlya
grammokban)
(A sűrűség SI mértékegységei kg/m3, g/cm3,
kg/dm3 ; a fajsúly SI mértékegységei N/cm3, kN/dm3, MN/m3)
Szilárd testek
| acél |
7,8-7,9 |
| alumínium |
2,72 |
| arany |
19,29 |
| agyag |
1,9-2,6 |
| beton (kavicsos) |
1,8-2,45 |
| cement |
0,82-1,95 |
| cukor |
1,6 |
| Fa (száraz) |
|
| tölgy |
0,69 |
| fenyő |
0,52 |
| bükk |
0,73 |
| homok (száraz) |
1,4-1,65 |
| homok (nedves) |
1,9-2 |
| kavics |
1,8-2 |
| kősó |
2,1-2,4 |
| ólom |
11,34 |
| ón |
7,3 |
| papír |
0,7-1,2 |
| parafa |
0,2-0,35 |
| platina |
21,5 |
| réz |
8,93 |
| tégla |
1,4-1,6 |
| ablaküveg |
2,1-2,5 |
Folyadékok
| alkohol |
0,789 |
| benzin |
0,7 |
| diesel-olaj |
0,85-0,88 |
| glicerin |
1,256 |
| kénsav
(100%) |
1,83 |
| petróleum |
0,8-0,82 |
| tengervíz |
1,02-1,06 |
| terpentinolaj |
0,855 |
Gázok
1 m3 (1000 liter) normális (1 atmoszféra) nyomású
és 0 C°-ú gáz súlya
grammokban
Mi van a világűrben?
Teljesen üres-e a világtér? Hiányoznak-e onnan az anyagok legapróbb részecskéi?
Nem! A bolygóközi, a csillagközi tér sem üres. Ott az anyag igen ritka eloszlású,
az anyag sűrűsége roppant kicsiny. Erről az a számadat tájékoztat bennünket,
hogy:
A csillagközi térben átlagosan ezermillió köbkilométer térfogatban mindössze
1 gramm anyag található.
Kíváncsiak vagyunk a másik végletre is: van-e a világegyetemben sűrűbb anyag
is, minta legsűrűbb földi anyag,
a 22,5 sűrűségű ozmium?
Bőségesen! Például a csillagászok számítása szerint vannak olyan csillagok,
amelyeknek átlagos sűrűsége 300 000 gramm köbcentiméterenként. Ha egy gyűszűnyi
(5 cm3) anyagot elhoznánk erről a csillagról, ez a Földön 1500 kilogrammot,
(15 métermázsát) nyomna!
Pedig még az ilyen óriási sűrűségű
anyagban is nagyon
lazán vannak egymás mellett az anyag
részecskéi. Ez a sűrűség,
semmiség ahhoz a szélső határhoz képest, amikor egyetlen gyűszűben 50 millió
métermázsa anyagot
kellene elképzelnünk. - Vagy még szemléletesebben: egyetlen gyűszűben kétezer
(egyenként ezertonnás) tehervonat anyagát
kellene összesűríteni.
Ilyen sűrűségű anyaghoz akkor jutnánk, ha sikerülne az anyagok atomjainak magját
úgy egymás mellé rakni, hogy érintkezzenek.
Meg tudnánk magyarázni
az anyag legkisebb részecskéinek, az atomoknak és a molekuláknak segítségével
azt a tényt, hogy a különféle anyagok fajsúlya különböző nagyságú? Például:
miért majdnem 7-szer akkora az arany fajsúlya (19,29), mint az alumíniumé (2,72)?
Mivel a különböző anyagok legkisebb részecskéinek, az atomoknak, a molekuláknak
a súlya különböző, azért a belőlük álló anyagok fajsúlyának is különböző nagyságúnak
kell lennie..
Hozzájárul ehhez még az is, hogy az egyes anyagok legkisebb részecskék, az atomok,
molekulák különböző nagyságúak. Ezért az egyik anyagban jobban összezsúfolódnak,
a másikban kevésbé.
Melyik nyomható össze könnyebben: az acél vagy a víz?
Mi történik akkor, ha az acélt vagy a vizet összenyomjuk?
Legkisebb részecskéik közelebb kerülnek egymáshoz, több jut belőlük egy köbcentiméternyi
térbe. Ezért nagyobb lesz az összenyomott anyag sűrűsége és a fajsúlya.
Hol vannak egymáshoz közelebb a legkisebb részecskék, az acélban vagy a vízben?
Természetes, hogy a szilárd testben, az acélban. Ha tehát ezeket az egymáshoz
már úgyis közel levő részecskéket még közelebb akarjuk nyomni egymáshoz, akkor
az acélban a részecskék jobban ellenállanak, kevésbé közelednek egymáshoz, mint
a folyadékokban.
A kísérlet azt mutatja, hogy ha ugyanakkora nyomást gyakorolunk az acélra és
a vízre, akkor az acél térfogatának megváltozása 32-szer kisebb, mint a vízé!
De ha a testek anyagának térfogata egyre kisebbedik, akkor sűrűségűk nagyobb
lesz. Ha például a vizet eredeti térfogatának felére, harmadára sikerülne összenyomni,
akkor sűrűsége kétszer, háromszor akkora lenne, mint volt. Az olyan vízben,
amelynek sűrűsége 3 volna, már az alumínium is úsznék, mert az alumínium sűrűsége
csak 2,7.
Lebegve maradhat-e a hajóroncs a tenger mélyén?
Vannak a tengerben 10 kilométernél nagyobb mélységek is. Sőt 1960. január 23-án
Piccard és Walsh öt óráig tartó merülés után 11 510 méter mélybe, a tengerfenékre
szálltak alá készülékükkel.
Ilyen mélységben a tárgyakat, tehát a tenger vizét is a felettük levő, 10 kilométernél
is magasabb vízoszlop nyomja.
Igaz-e, hogy Ilyen nagy nyomás alatt a tengervíz annyira összeszorul, sűrűsége
annyira megnövekedik, hogy a víz
sűrűsége nagyobb lesz, mint a fémeké és még a fémek sem merülnek a tengerfenékre,
hanem a vízben lebegve
maradnak?
Ezt a kérdést valóban gyakran felvetik vitatkozó társaságokban.
A felelet: még a legmélyebb tengerfenéken levő víz
is csak olyan kevéssé nyomódik össze, hogy sűrűsége még 1,1 sem lesz, és nemcsak
a fémek süllyednek a fenékre, hanem még mahagóni és egyéb fafajták is, amelyeknek
fajsúlya nagyobb
mint 1,1.
Hogyan lehet bebizonyítani azt, hogy a tengervíz sűrűsége
a legmélyebb tengerrész fenekén sincs még 1,1 sem?
Kísérlettel. Ha 1 cm2 vízszintes lap fölé 10 kilométer (1 millió centiméter)
magas vízoszlopot helyezünk, ennek súlya 1 millió gramm = 1000 kilogrammsúly
lesz. Tehát 10 kilométer mélységben a víz nyomása 1000 kilogrammsúly, 1000 atmoszféra.
Van készülékünk, amelynek segítségével a vizet 1000 kilogrammsúly nyomás alá
helyezhetjük. Azt tapasztaljuk, hogy a víz térfogata körülbelül 5%-kal lesz
kisebb, tehát sűrűsége is mintegy 5%-kal növekedik.
Ez valóban jelentéktelen sűrűségváltozás. Hiszen ha a legsósabb tengervíz 1,06
sűrűsége 5%-kal nő, még akkor is csak 1,06 + 0,05 = 1,11 ~ 1,1 lesz a víz sűrűsége
10 000 méter mélységben.
Lehet-e látni a molekulákat?
Már említettük a molekulák
nagyságát. Vonalas kiterjedésük körülbelül az egymilliomod milliméter és ennek
tizedrésze közé esik. Ha milliószoros nagyítást
alkalmaznánk, akkor az átlagos molekula,
például a szódavízben
levő szén-dioxid molekulája
körülbelül fél milliméter nagyságúnak látszana. De nincs szükség ekkora nagyításra,
mert a már ötször kisebb tárgyat, az egytized millimétereset is meglátjuk. Tehát
az egymilliószoros nagyítás
helyett az ötször kisebb, a 200 000-szeres nagyítás
is láthatóvá teszi a molekulákat.
Elektronmikroszkóppal
elérték a 200 000-szeres nagyítást.
Az átlagos nagyságú molekula
már meglátható vele. Ámde a kaucsuk,
a tojásfehérje és
más anyagok molekulái,
az úgynevezett óriásmolekulák
sok milliószor nagyobb tömegűek is lehetnek, mint az átlagos molekulák.
Ezek már néhány tízezerszeres nagyításban
is akkorának látszanak, mint az apró kukacok. A fénymikroszkóp
azért nem alkalmas, mert hasznos nagyítása
még az ezerszereset sem éri el.
Felhasznált irodalom
 Tegyük fel, hegy egy gyűrű anyaga ezüst és arany ötvözete. Ha a gyűrű fajsúlya
14, akkor a gyűrű súlyának felét arany alkotja. De ha a gyűrű fajsúlya több
mint 14, akkor 50%-nál több benne az aranytartalom. Ha pedig a gyűrű fajsúlya
ennél kisebb, akkor 50%-nál kevesebb arany van benne.
Tegyük fel, hegy egy gyűrű anyaga ezüst és arany ötvözete. Ha a gyűrű fajsúlya
14, akkor a gyűrű súlyának felét arany alkotja. De ha a gyűrű fajsúlya több
mint 14, akkor 50%-nál több benne az aranytartalom. Ha pedig a gyűrű fajsúlya
ennél kisebb, akkor 50%-nál kevesebb arany van benne.